Gamma matrices and Gell-Mann's I - Y categorization

[James1238765]

TL;DR Summary

What do the gamma matrices aside from $\gamma_3 (I)$ and $\gamma_8 (Y)$ represent in SU(3)?

As there was quite rightly some criticism earlier about not following proper theory, I will first demonstrate what I have understood of the gamma matrices of SU(3).

There are 8 gamma matrices that together generate the SU(3) group used in QCD. Gell-Mann used only 2, $\gamma_3$ and $\gamma_8$, to great effect, by defining:

$$ I = \frac{1}{2} \gamma_3 =
\begin{bmatrix}
\frac{1}{2} & 0 & 0 \\
0 & -\frac{1}{2} & 0 \\
0 & 0 & 0
\end{bmatrix} $$
and
$$ Y = \frac{1}{2\sqrt3} \gamma_8 =
\begin{bmatrix}
\frac{1}{3} & 0 & 0 \\
0 & \frac{1}{3} & 0 \\
0 & 0 & -\frac{2}{3}
\end{bmatrix}
$$

These two definitions of Y and I completely determine all the following classifications for mesons and baryons:

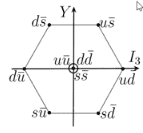
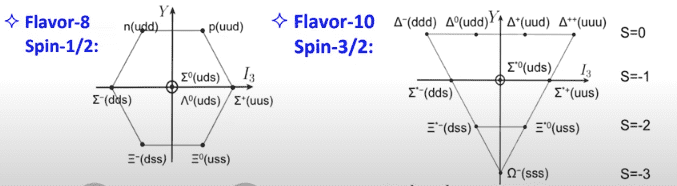
For instance, by first defining $uud$ as:

$$ uud =
\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix} +
\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix} +
\begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix} =
\begin{bmatrix}
2 \\
1 \\
0
\end{bmatrix}$$

we obtain

$$
I(uud) =
\begin{bmatrix}
\frac{1}{2} & 0 & 0 \\
0 & -\frac{1}{2} & 0 \\
0 & 0 & 0
\end{bmatrix}

\begin{bmatrix}
2 \\
1 \\
0
\end{bmatrix} =
\begin{bmatrix}
1 \\
-\frac{1}{2} \\
0
\end{bmatrix} =

1 - \frac{1}{2} + 0 = \frac{1}{2}$$

and

$$
Y(uud) =
\begin{bmatrix}
\frac{1}{3} & 0 & 0 \\
0 & \frac{1}{3} & 0 \\
0 & 0 & -\frac{2}{3}
\end{bmatrix}

\begin{bmatrix}
2 \\
1 \\
0
\end{bmatrix} =
\begin{bmatrix}
\frac{2}{3} \\
\frac{1}{3} \\
0
\end{bmatrix} =
\frac{2}{3}+\frac{1}{3}+0 = 1$$

Thus, the coordinate of $uud$ is $[\frac{1}{2}, 1]$. All other elements are checked to be mapped correctly into the graph above.

From these 2 fundamental $I$ and $Y$ definitions, dependent quantities like charge and mass can be constructed as follows:

$$ Q = I + \frac{Y}{2}$$
$$ M = a_0 + a_1 Y + a_2 (I(I+1) - \frac{Y^2}{4})$$

for some constant $a_0, a_1$ and $a_2$.

This allowed for the prediction of a new particle $sss$, which were later discovered having the correctly predicted mass. This $I - Y$ categorization of the particles was awarded the Nobel Prize in 1969.

This is where many presentations end on Gell-Mann's categorization. My question is, given that there are 6 more thus far unused basis of SU(3), $\gamma_1, \gamma_2, \gamma_4, \gamma_5, \gamma_6, \gamma_7$, what do each of these gamma matrices represent, and what further categorizations can be achieved by employing these other matrices aside from $\gamma_3$ and $\gamma_8$?

 

[malawi_glenn]

You are mixing SU(3) flavor and SU(3) color, two different symmetries. SU(3) flavor is an (approximate) global symmetry and SU(3) color is an exact local (gauge) symmetry.

It is still not clear to me, what you really want to know. Do you want to know about SU(3) and Gell-mann matrices in hadron physics or in QCD?

 

[James1238765]

@malawi_glenn thank you. It felt quite odd when the Intro to QCD presentations all talked about u, d, s. So there are two symmetries for color and flavor. What happens now that there are 6 quarks u,d, s, c, t, b?

 

[malawi_glenn]

What happens now that there are 6 quarks u,d, s, c, t, b?

Then flavor SU(N) is no longer approriate to describe Hadron states.
b.t.w top quarks do not form bound states, they live too short.
SU(3) global flavor symmetry is used to (approximate) the lightest hadrons, because u d and s quarks are "much" lighter than the QCD-condensation mass/energy scale.

It felt quite odd when the Intro to QCD presentations

which ones?

 

[vanhees71]

I think the OP is only looking at the (approximate) flavor symmetry SU(3), i.e., Gell-Mann and Zweig's "eightfold way".

The idea is to group the hadrons (mesons and baryons) according to the representations of SU(3). What you call $\gamma$ matrices is usually called the $\lambda$ matrices (not to confuse them with the Dirac $\gamma$ matrices of the $(1/2,0) \oplus (0,1/2)$ representation of the Poincare group, used to describe spin-1/2 fermions.

Since SU(3) is a compact semisimple Lie group you can one-to-one map its representations to the unitary representations of its Lie algebra su(3), which in the fundamental representation are spanned by the 8 Gellmann matrices $\lambda_k$, out of which two are commuting, which are $\lambda_3$ and $\lambda_8$. There are no more linearly independent matrices out of su(3) that commute with these two. So you have two additive charge-like quantum numbers, denoting the isospin (the eigenvalues of $\lambda_3/2$ from the su(2) sub-algebra spanned by $\{\lambda_1,\lambda_2,\lambda_3 \}$) and "hypercharge" (the eigenvalues of $Y$).

The fundamental representation $\textbf{3}$ belongs to the quarks, its conjugate complex representation $\bar{\textbf{3}}$ to the anti-quarks (these two three-dimensional representations are not equivalent in contradistinction to the more familiar SU(2)), and you can get all representations by tensor products of these two fundamental representations, which can be decomposed in the irreducible ones.

 

[James1238765]

@vanhees71 thank you. The spelled-out names and properties are really helpful to learn/check on.

 

[malawi_glenn]

Greiners book on "quantum mechanics symmetries" is a good reference if you can borrow it from a library.

OP also mentioned gluons (in their other recent thread). Are you still interested in that?

 

[PeterDonis]

many presentations

What presentations? Please give specific references.

 

[malawi_glenn]

By showing your references, we can help further explain and help your lack of misunderstanding

 

[James1238765]

@malawi_glenn @PeterDonis thank you. I watched plenty of presentations, it was a sort of amalgam of the parallel derivations. I think i shall try to look into the SU(3) group for gluons next.

 

[PeterDonis]

I watched plenty of presentations, it was a sort of amalgam of the parallel derivations.

So which presentations? You need to at least give us some references.

 

[PeterDonis]

These two definitions of Y and I completely determine all the following classifications for mesons and baryons

Where do the diagrams you posted come from?

 

[PeterDonis]

So which presentations? You need to at least give us some references.

Where do the diagrams you posted come from?

@James1238765 apart from the fact that references should always be given here upon request, there are two other reasons you need to respond to these questions: first, the description you give in the OP is questionable, so we need to know where it came from; second, the images you posted in the OP might be under copyright, in which case you shouldn't be posting them, you should be linking to the source.

 

[James1238765]

@PeterDonis The links I remembered are:




(the diagrams)


and some pdf papers (I could not remember all).

If you are wondering about the explicit matrix calculations, I did them myself as a test and found all the elements to map correctly. The sum $1 - \frac{1}{2} + 0$ of the vector components is invented.

 

[PeterDonis]

If you are wondering about the explicit matrix calculations, I did them myself as a test and found all the elements to map correctly.

That's just luck because the matrices are diagonal. What is actually going on is not what you calculated.

The sum $1 - \frac{1}{2} + 0$ of the vector components is invented.

Please be advised that personal theories are off limits at PF. You can't just "invent" things.

 

[James1238765]

@PeterDonis RE the many entanglement questions permeating.

 

[PeterDonis]

The links I remembered are

What about the images you posted in the OP?

 

[PeterDonis]

@PeterDonis RE the many entanglement questions permeating.

What does this mean?

 

[PeterDonis]

If you are wondering about the explicit matrix calculations, I did them myself as a test and found all the elements to map correctly.

In the OP you say Gell-Mann used the $\lambda_3$ and $\lambda_8$ matrices (I use those symbols instead of the ones you used in the OP for reasons that were posted earlier) to generate the $I_3$ - $Y$ classification. Where did you get that from? Please give a reference. It's not in any of the videos you referenced, as far as I can tell.

 

[James1238765]

@PeterDonis I meant that most questions/posts being asked are already superimposing personal understanding (or "invented theories" if you will), and asking for clarification. If the understanding is not correct, I believe it is sufficient to point out the factual errors, and reasons why this formulation is not correct...

 

[PeterDonis]

I meant that most questions/posts being asked are already superimposing personal understanding (or "invented theories" if you will), and asking for clarification.

Asking questions about your personal understanding of some aspect of standard physics is one thing. That's fine here.

Making up your own calculations and then asking questions about them as if they were part of standard physics is quite another, and is not fine here, it's off limits. And that is what you are doing.

 

[PeterDonis]

Thread closed for moderation.

 

[PeterDonis]

After moderator discussion, this thread will remain closed.