(1) About that user name. I met Feynman. You're no Feynman.
(2) The fact that you couldn't give an answer to
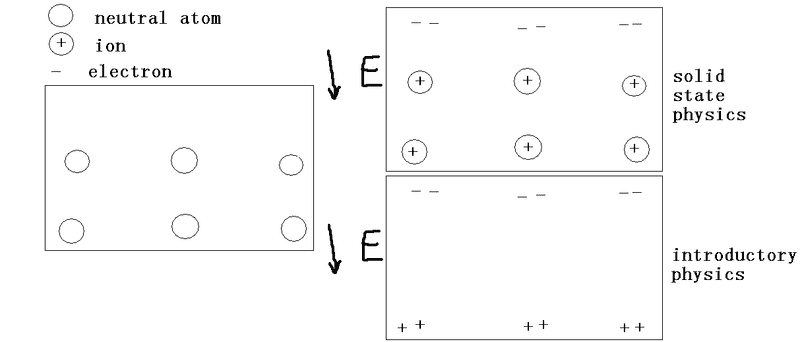
@berkeman 's entirely reasonable question of where you read this is telling. It suggests the misunderstanding lies with you can not the textbooks. I know of no textbook that says positive ions in a metal move in an electric field (your bottom drawing). If you know of one, say so, not just the vague and unactionable (and likely incorrect) "any introductory physics textbook."
(3) You keep groping towards the century-discredited Drude model, where electrons behave as a classical gas. As we said in your last thread on this, a classical theory of electromagnetism, where charge is treated as a continuous fluid will work (in its domain of validity). A quantum-mechanical treatment of electrons will work. Mixing the two, as you are trying to do, will not work. A classical treatment of electrons, inherently a quantum mechanical object, cannot give the right answer.