- #1
Saitama
- 4,243
- 93
Homework Statement
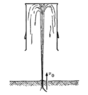
An inverted garbage can of weight W is suspended in air by water from a geyser. The water shoots up the ground with speed ##v_0##, at a constant rate ##dm/dt##. The problem is to find the maximum height at which garbage can rides. What assumption must be fulfilled for the maximum height to be reached.
Ans. clue. If ##v_0=20\, m/s##, W=10kg, dm/dt=0.5 kg/s, then ##h_{max} \approx 17 \, m##
Homework Equations
The Attempt at a Solution
I don't know how to begin with this problem. I think that I have to find the force due to water but I can't see how to form the equations here. I need a few hints to begin with.
Any help is appreciated. Thanks!