Gauss-Jordan Elimination algorithm steps

[member 731016]

Homework Statement

Please see below

Relevant Equations

Row operations

For this problem,

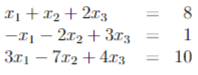
For (i) the solution is,

However, I am somewhat confused how to follow the steps of the Gauss-Jordan Elimination algorithm from there. Do I have to eliminate the coefficients from $x_2$ and $x_3$ respectively from row 1 and the -5 coefficient from row 2 in the exact order that they did?

For example, could I do for the First row $R_1 - R_2$ which would transform the first row to $(1~0~7~:~17)$ then do row operations to make the top two values in the third column to become zero?

Thank you for any help.

Many thanks!
Many thanks!

 

[Steve4Physics]

For this problem,
View attachment 324955
View attachment 324956
For (i) the solution is,
View attachment 324959
However, I am somewhat confused how to follow the steps of the Gauss-Jordan Elimination algorithm from there. Do I have to eliminate the coefficients from $x_2$ and $x_3$ respectively from row 1 and the -5 coefficient from row 2 in the exact order that they did?

Yes (I guess).

For example, could I do for the First row $R_1 - R_2$ which would transform the first row to $(1~0~7~:~17)$ then do row operations to make the top two values in the third column to become zero?

It will lead to the correct answer but (I guess) it is probably not what is required.

There are many possible sequences of row operations which would give the correct RREF. But from the wording in the question, it appears you are required to use the specific approach as shown in the model answer.

This would make sense if, for example, it’s part of a computer-science course where you might be required to write some code for this.

The algorithm used in the model answer is, in essence, this:

1. From the top down, repeat for each Row:

a) if needed, multiply the Row so that its left-most non-zero entry is set to 1; this is the Pivot for this Row;

b) add/subtract multiples of the Row from the rows beneath it, to make all values below the Pivot equal to zero.

You end up with 1s in the pivot positions and all zeroes to the left of the pivots.

2. From the bottom up, repeat for each Row:

add/subtract multiples of the Row from the rows above it, to make all values above the Row’s pivot equal to zero.

You end up with RREF.

That's a non-rigorous description.

Note, in this question, no rows initially have leading zeroes. If they did, the initial step would have been to re-order the rows so that the rows with most leading zeroes are nearest the bottom.

Edit - typo's.