Gauss' law and an object with nonuniform charge distribution

[Leo Liu]

Gauss' law: $$\iint_{\partial A}\vec E\cdot d\vec A=\frac{Q}{\epsilon_0}$$

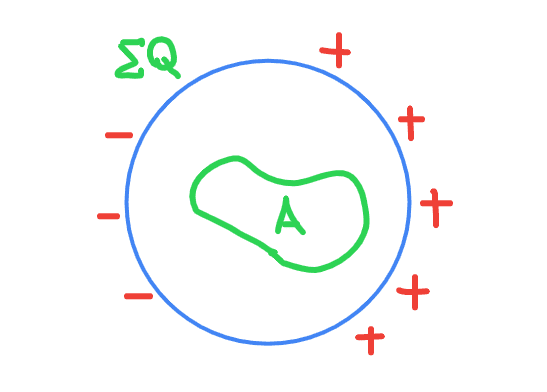
Suppose we have a unevenly charged non-conducting spherical shell, in which a Gaussian surface is placed. In this case, is the electrical field on A 0, given that there is no charge inside A? I came up with this example to ascertain whether the G's law applied to a body with nonuniform charge distribution.
Thanks.

EDIT: In hindsight, I realized I asked a very dumb question. Sorry for wasting the time of all of us. Haha.

 

[Ibix]

Gauss' law does not say that the field is zero - it says (roughly) that the component of the field perpendicular to the Gaussian surface, summed over the whole surface is zero. Your charge distribution looks like a parallel plate capacitor, just with the plates a bit bent. Is the electric field inside a capacitor zero?

An actual parallel plate capacitor is easier to understand. Draw a parallel plate capacitor with very large plates. What does the electric field look like? Draw a Gaussian surface that is a long thin rectangle, with the long side parallel to the plates. Which way does $d\vec A$ point on each of the four sides? So what is $\vec E.d\vec A$ on each of the four sides? So what is the integral over the whole surface?

 

[Leo Liu]

Right. Let's put this imaginary gigantic capacitor, whose left plate carries positive charge on a plane so that its gap is parallel to the y axis. Then the electric flux flowing through the left side of the rectangle is $\mathbf{\Phi}_l=QA/\epsilon_0\;\hat i$, and the flux passing through the right side of the rectangle is $\mathbf{\Phi}_r=-QA/\epsilon_0\;\hat i$. It follows that the total flux summed over the closed surface is 0, suggesting that there is no charge inside the rectangle.

 

[Ibix]

That's right. The field isn't zero (nor is it in your original diagram), but the integral of the field dotted with the vector area is zero. It means that if you draw field lines you'll find that any field line that crosses the surface crosses it again somewhere in the opposite direction. That isn't the case with a surface that encloses net charge, because field lines will start on the charge and at least some will go out to infinity, crossing the surface only once (or some other odd number of times if your surface is complicated).

 

[Leo Liu]

That's right. The field isn't zero (nor is it in your original diagram), but the integral of the field dotted with the vector area is zero. It means that if you draw field lines you'll find that any field line that crosses the surface crosses it again somewhere in the opposite direction. That isn't the case with a surface that encloses net charge, because field lines will start on the charge and at least some will go out to infinity, crossing the surface only once (or some other odd number of times if your surface is complicated).

Is it correct to say that, mathematically, the divergence of the electric field is 0 when there is no charge inside, and is nonzero when there is a charge inside which acts as a faucet or a sink?

 

[vanhees71]

It's always simpler to think in terms of the differential form of Maxwell equations. One is Gauss's Law for the electric charge,
$$\vec{\nabla} \cdot \vec{E}=\frac{1}{\epsilon_0} \rho,$$
which means that the source of the electric field are electric charges.

 

[Ibix]

Is it correct to say that, mathematically, the divergence of the electric field is 0 when there is no charge inside, and is nonzero when there is a charge inside which acts as a faucet or a sink?

Not quite. The divergence of a field is defined at a point, whereas the integral form of Gauss' law is defined over a volume. So if you have a volume that includes a negative charge (gives a positive divergence at that point) and an equal positive charge (negative divergence at that point), the integral of divergence over the volume can be zero even if the divergence isn't zero everywhere.

So it is correct to say that if the integral $\iint_S\vec E\cdot d\vec A$ over a closed surface $S$ is zero then the total divergence over the enclosed region is zero, but not necessarily that the divergence is everywhere zero.

 

[alan123hk]

I think Gauss's law states that the flux of the electric field out of an arbitrary closed surface is proportional to the total charge enclosed by that surface, no matter how the charges are distributed and how fast they are moving.

That is, even if the total electric flux through the closed surface is zero, in this case, the total charge inside must be zero, but there can still be positively charged objects, negatively charged objects and electric fields inside the closed surface.

 

[vanhees71]

Of course the integral form follows from the differential form (and vice versa) via Gauss's Integral Theorem,
$$\frac{Q_V}{\epsilon_0}=\int_{V} \mathrm{d}^3 x \vec{\nabla} \cdot \vec{E}=\int_{\partial V} \mathrm{d}^2 \vec{f} \cdot \vec{E}.$$
So the "flux" of the electric field through a closed surface is the charge within the enclosed volume (modulo a unit-conversion factor $1/\epsilon_0$).