annamal
- 393
- 33
- Homework Statement
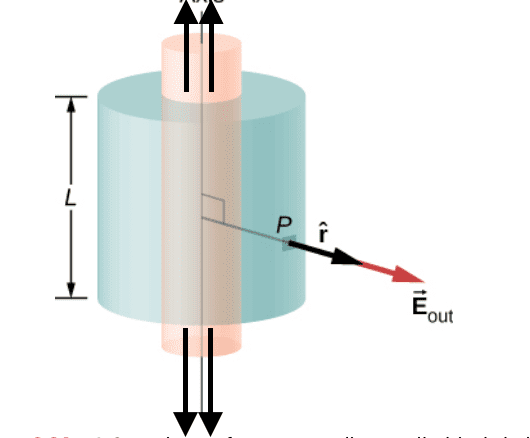
- A very long non-conducting cylindrical shell of radius R has a uniform surface charge density ##\sigma##. Find the electric field at a point outside the shell.
- Relevant Equations
- ##\frac{R\sigma}{\epsilon_0*r}##
I am confused why we don't take into account the lids of the cylinder since the Gaussian cylinder is of finite height L as shown in the image