Gaussian probability distribution of formation PBH

[koulbichok]

Hello. If we consider PBH formation from collapse of large density perturbation in the early Universe, a mass PBH depends on density contrast as

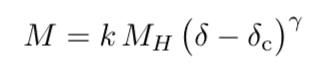
And δ must be larger then

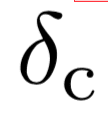. Also we have β — an abundance of black holes, it's the ratio of the PBH energy density to the total energy density, this is defined as

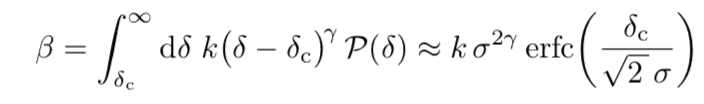
Where P(δ) is Gaussian, which describes a perturbation profile and hence the probability of black hole formation with current δ.

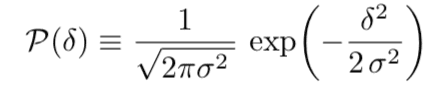
So, I have a problem with σ. I know this is average value of density contrast and might depends on particle Horizon mass, but I don't know how to find σ.

 

[AndyW]

Hello, thank you for bringing up this interesting topic. The parameter σ is the root mean square (RMS) density contrast and can be calculated using the power spectrum of density fluctuations in the early Universe. This power spectrum can be obtained from cosmological models and observations of the cosmic microwave background radiation. The exact value of σ depends on the specific cosmological model and the scale at which you are considering the density fluctuations. For PBH formation, it is important to consider the density fluctuations on small scales, typically corresponding to the horizon mass. I recommend consulting with a cosmologist or referring to literature on cosmological models to obtain a more precise value for σ in your specific scenario. Additionally, it is important to note that the value of σ may also be affected by other factors such as the equation of state of the early Universe and the presence of other forms of matter or energy. I hope this helps to clarify your understanding of σ and its role in PBH formation.