- #1
trulyfalse
- 35
- 0
Hello PF! I'm having trouble approaching this problem. Any assistance would be greatly appreciated.
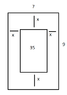
A rectangle with area of 35 cm2 is formed by cutting off strips of equal width from a rectangular piece of paper. The rectangular piece of paper is of 7cm width and 9cm length.
ax2+bx+c
I know that I have to create two separate equations and substitute to solve, however I'm really not certain how to create those equations (more-so what to base them on) . Perhaps a push in the right direction is all I require...
Homework Statement
A rectangle with area of 35 cm2 is formed by cutting off strips of equal width from a rectangular piece of paper. The rectangular piece of paper is of 7cm width and 9cm length.
Homework Equations
ax2+bx+c
The Attempt at a Solution
I know that I have to create two separate equations and substitute to solve, however I'm really not certain how to create those equations (more-so what to base them on) . Perhaps a push in the right direction is all I require...