Generalized coordinates and the Lagrangian

[GLD223]

Homework Statement

Find the degrees of freedom of the system with the given PE. What are the variables of integration? Find the Lagrangian using the generalized coordinates.

Relevant Equations

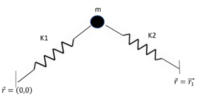
$PE = 1/2 * k_1 * R^2 + 1/2 * k_2 * (\vec{r} - vec{r_1})^2$ note that $r$ and $r_1$ are vectors

So I think the mass can only move in two "coordinates" the axis of which the mass is connected to $k_1$ and the axis connecting it to $k_2$. Therefore, the D.O.F is 2. I don't understand what it the meaning of "variables of integration" What does it mean?
Apart from that, I attempted to solve for the Lagrangian:
$T = 1/2 * m * v_m^2$
V is given
$v_m = d/dt(x_m)$
$x_m = 1/2 * \vec{r_1} + something* \hat{y} = 1/2 * r_1 * \hat{x} + something* \hat{y}$
I have no clue how to solve this. Any help would be appreciated

 

[BvU]

Hi,
The problem statement is a complete mystery. No idea what $R$ is, nor what $\vec r$ is. Is $\vec r_1$ fixed? Given?

Sort out your notation. V is given means V=PE ?

$x_m$ ? "$something$" ?

$\$