Generalized parton distributions

[humanino]

In some of my previous posts, I referred to GPDs, a recently developped formalism describing hadronic states. I am afraid that this formalism remains largely ignored partly because few introduction review are only recently available.

See for instance :
Markus Diehl, Phys.Rept. 388 (2003) 41-277, hep-ph/0307382
Link to Markus' thesis
and references therein. I especially also like Ji's papers.

Since this a lengthy paper, I feel it is not useless that I write here some infos I think give motivations for it. The following is schematic. It only intends to lead as fast as possible to the formalism of GPDs. I hope this is not going to be considered as spamming

The early data on the nucleon (hadronic) structure came mainly from Elastic Lepton Scattering (ELS) $$lN\rightarrow l'N'$$ or from Deep Inelastic Scattering (DIS) $$lN\rightarrow l'X$$ with the final hadronic state $$X$$ undetermined. ELS and DIS seem at first rather difficult to unify, although a satisfactory understanding of the nucleon structure would require such a full picture. ELS provides access to the usual Elastic Form Factors (EFF) : Dirac $$F_1(t)$$, Pauli $$F_2 (t)$$, axial $$g_A(t)$$ and pseudoscalar $$g_P(t)$$. For each of the quark species, they parameterize the electroweak vertex :

$$\langle p'|\bar{q}(0)\gamma^\mu q(0)|p\rangle = \bar{u}(p')\left[ F^q_1(t)\gamma^\mu + F^q_2(t)\frac{\imath \sigma^{\mu \alpha}\Delta_\alpha}{2m} \right] u(p)$$
$$\langle p'|\bar{q}(0)\gamma^\mu\gamma_5 q(0)|p\rangle = \bar{u}(p')\left[ g^q_A(t)\gamma^\mu\gamma_5 + g^q_P(t)\frac{\gamma_5\Delta^\mu}{2m} \right] u(p)$$
​

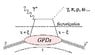
with $$\Delta = p'-p$$ and $$t=\Delta^2$$ as usual. On the other hand, DIS provides the quark distributions $$q(x)$$ and helicity distributions $$\Delta q(x)$$ with respect to Bjorken's $$x$$ scaling variable, interpreted as the momentum fraction carried by the struck quark in the so-called infinite momentum frame : $$x\in[0,1]$$ In DIS restricted to the EM probe (not the full electroweak interaction involving the Z in neutral currents and the W in charged currents as well), the optical theorem relates the cross-section to the imaginary part of the forward Compton amplitude : ( cf theoroptq.jpg : The Feynmam graph on the LHS omits the leptons $$l$$ and $$l'$$.) The optical theorem here is only a mean of calculation to avoid the sum over $$X$$ : the forward Compton process is not kinematically allowed !

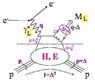
The introduction of GPDs relies on physical process corresponding not merely to quark distributions, but to quark correlations. Such processes are the Deeply Virtual Compton Scattering (DVCS), or the Deeply Virtual Meson Production (DVMP) : (cf GPDs.jpg).

The important property of Quantum Chromo-Dynamics (QCD) called factorization allows one to separate a process into a hard subprocess involving only one parton and calculated with perturbative techniques in the standard Quantum Electro-Dynamics (QED) or perturbative QCD (pQCD) framework, and a soft subprocess encoding the non-perturbative physics of the proton structure and in our case parameterized by the GPDs. The validity of factorization relies on theorems specifying a large scale limit, such as a large momentum transfer, or a large virtuality of a probing particle for instance. The GPDs are non-forward (off-diagonal or skewed) matrix elements because they appear in an amplitude relating two-parton states of the form $$\Psi^*(x-\xi)\Psi(x+\xi)$$, as compared to ordinary parton distributions $$q(x)$$ and $$\Delta q(x)$$ which are diagonal operators $$\Psi^*(x)\Psi(x)$$.

We compare the diagram for Deeply Virtual Compton Scattering (DVCS) (called "handbag" diagram) and the diagram for DIS, related to a diagonal matrix element through the optical theorem. The DVCS process requires a nonzero momentum transfer between the initial and final nucleons. The matrix element $$\Psi^*(x-\xi)\Psi(x+\xi)$$ must be properly defined in a convenient gauge where the Wilson gauge link along the light-cone is the identity, and using the nonlocal operator product expansion with respect to the order $$\tau$$ called twist and defined as $$\tau = d_{ O} - s_{ O}$$ where $$d_{ O}$$ is the dimension of the operator $$\Psi^*(x-\xi)\Psi(x+\xi)$$ and $$s_{ O}$$ is its spin. At lowest twist (i.e. 2), each parton species (quarks and gluons) has two quark helicity dependent GPDs denoted $$\tilde{H}(x,\xi,t)$$ and $$\tilde{E}(x,\xi,t)$$, as well as two quark helicity averaged GPDs denoted $$H(x,\xi,t)$$ and $$E(x,\xi,t)$$. They depend on the average longitudinal momentum fraction $$x$$ of the parton involved in the hard subprocess, the longitudinal momentum transfer $$\xi$$ between the initial and final parton, and the squared four-momentum transfer $$t$$. In this context, a negative value of the longitudial momentum fraction $$x$$ corresponds to an antiquark. Two more GPDs $$H_T$$ and $$\tilde{H}_T$$ are needed when one includes parton helicity flip. The GPDs $$q^2$$ evolution interpolates between the DGLAP regime of parton density and the ERBL sector of meson amplitudes. The first $$x$$ moment of the GPDs allows one to recover the usual proton's form factors (Dirac, Pauli, axial, and induced-pseudoscalar). At $$\xi=t=0$$, the GPDs $$H$$ and $$\tilde{H}$$ reduce to the quark longitudinal momentum and helicity distributions $$q(x)$$ and $$\Delta q(x)$$. New physics is available in the kinematical region $$-\xi<x<\xi$$, a regime in which GPDs probe $$q\bar{q}$$ and gluons pairs, and are thus sensitive to the dynamics of sea quarks and meson degrees of freedom. The $$t$$ dependence is related to the transverse spatial distributions of partons in the nucleon. Thus, mapping out the GPDs will allow for the first time a full 3-dimensional picture of the proton. Finally, Ji's sum rule (the second moment relative to $$x$$ of the sum $$H+E$$ equals the total angular momentum carried by the quarks) will settle the issue of the spin of the proton, by providing a measure of the total contribution of quarks to the spin of the proton, including orbital angular momentum. Even more, GPDs furnish access to the Energy-momentum tensor of each parton species ! The only other known way to obtain this information is graviton scattering. One experimental evidence for this GPD formalism to hold is to look for the $$q^2$$ behavior of the cross sections and other observables, which should follow definite scaling laws. DVCS is perceived as the cleanest process to experimentally access the GPDs, because the hard part of the process involves only electromagnetic couplings.

 

[marlon]

Hi Humanino, sounds interesting...

I am especially interested in the second figure of this factorizationg thing out of QCD. I know this concept, but I donnot understand this diagramma very well, could you please elaborate more. What exactly happens there ? And what does what, you know, what are the force carriers ?

regards
marlon

 

[humanino]

Be careful with all my post which is not rigourous. I only wanted to give a reference as well as a scematic first view.

The second diagram is especially not rigourous. If the outgoing particle is a photon (DVCS), then everything is fine. But, as you can readily see in Markus' thesis, if the outgoing particle is a meson (DVMP), one needs another gluon propagator, as well as another blob corresponding to the amplitude for the meson to "bound". Attached is another more accurate diagram.

Here is a "must" text. It is older, and thus probably more difficult. But it is shorter.

Hard Exclusive Reactions and the Structure of Hadrons[/url]

 

[humanino]

Let me try to guess what happens, because nobody knows for sure

As you can see in these diagrams, as the electron gets near the nucleon one of the quarks in the bag happens to be in a state allowing him to interact : a virtual photon is exchanged, and the quark gets in an excited state, but promptly falls back in the bag emiting energy in the form of light (DVCS).

In the case of DVMP, things are slightly more complicated. The energy is realized in the form of an hadronic bound state, which is a vector meson.

The important point is : we contemplate correlations. Many many other things happen, but we want to select events in which the nucleon is still here in the outgoing channel. If this is the case, that means that the quark fell back inside. The big issue is that of course, the quark never really gets outside the bag (forbidden by confinement). The factorization theorems tell us that, during the interaction process, this one quark has ignored his usual buddies in the bag (all the other partons), and also that those other buddies could not affect the selected high-energy quark.

 

[humanino]

Waow
I wish I were born russian

Here is the latest, and most comprehensive, review on GPDs. Just in case anyone is interested

Unraveling hadron structure with generalized parton distributions
by A.V. Belitsky & A.V. Radyushkin

The generalized parton distributions, introduced nearly a decade ago, have emerged as a universal tool to describe hadrons in terms of quark and gluonic degrees of freedom. They combine the features of form factors, parton densities and distribution amplitudes--the functions used for a long time in studies of hadronic structure. Generalized parton distributions are analogous to the phase-space Wigner quasi-probability function of non-relativistic quantum mechanics which encodes full information on a quantum-mechanical system. We give an extensive review of main achievements in the development of this formalism. We discuss physical interpretation and basic properties of generalized parton distributions, their modeling and QCD evolution in the leading and next-to-leading orders. We describe how these functions enter a wide class of exclusive reactions, such as electro- and photo-production of photons, lepton pairs, or mesons. The theory of these processes requires and implies full control over diverse corrections and thus we outline the progress in handling higher-order and higher-twist effects. We catalogue corresponding results and present diverse techniques for their derivations. Subsequently, we address observables that are sensitive to different characteristics of the nucleon structure in terms of generalized parton distributions. The ultimate goal of the GPD approach is to provide a three-dimensional spatial picture of the nucleon, direct measurement of the quark orbital angular momentum, and various inter- and multi-parton correlations.