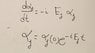- #1
Maximise24
- 33
- 1
This equation (see attachment) appears in one of Prof. Susskinds's lectures on Quantum Mechanics: in trying to differentiate the coefficients of the eigenvectors of a wave function with respect to time, an exponential e^(-iEt) is introduced for alpha.
I can see that d/dt e^(-iEt) = -iE e^(-iEt), but why is the second part e^(-iEt) not in the top equation in the attachment? Is it disregarded because it's just a number?
Thanks for any help provided!
I can see that d/dt e^(-iEt) = -iE e^(-iEt), but why is the second part e^(-iEt) not in the top equation in the attachment? Is it disregarded because it's just a number?
Thanks for any help provided!