Hardy
- 11
- 1
- TL;DR Summary
- Question about how to apply Taylor's Formula to a vector field to derive equation for divergence in cylindrical coordinates.
This is from an old E&M exam question where we were asked to derive the formula for the divergence of a vector field in cylindrical coordinates using Taylor's Approximation and the fundamental definition of the divergence:
The vector field, A, is defined in cylindrical components such that:
Where ρ, θ and z are the unit vectors in cylindrical coordinates, and Aρ, Aθ and Az are everywhere continuous and well defined functions.
The formula we are looking for (divergence in cylindrical coordinates):
I have found several similar analysis on-line, but most simply use the definition of the ∇ function in cylindrical coordinates and not Taylor's Formula. I am having a problem completing the analysis and it seems to stem from how Taylor's Formula is applied to the vector field. Hopefully the following is enough to convey the issue, I have lots more so that I could add if needed.
The vector field is represented by a Taylor's Series approximation about a point: Po(ρo,θo,zo)
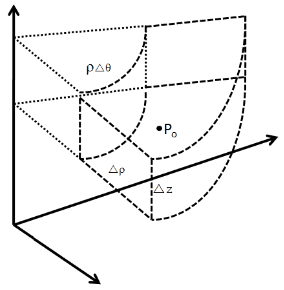
At this point I would apply Taylor's Formula such that:
A = AAAρ(Po)ρ + (ρ - ρo) (δ/δρ)(Aρρ) + (θ - θo) (δ/δθ)(Aρρ) + (z - zo) (δ/δz)(Aρρ)
A = + Aθ(Po)θ + (ρ - ρo) (δ/δρ)(Aθθ) + (θ - θo) (δ/δθ)(Aθθ) + (z - zo) (δ/δz)(Aθθ)
A = + Az(Po)z + (ρ - ρo) (δ/δρ)(Azz) + (θ - θo) (δ/δθ)(Azz) + (z - zo) (δ/δz)(Azz)
Which almost provides the correct answer, but not quite:
( 1/ρ ) (δ/δρ) (ρAρ) + ( 1/ρ ) { (δ/δθ)Aθ + Aθ } + (δ/δz)Az
Notice the only difference is the Aθ term.
But if I apply Taylor's Formula like:
A = AAAρ(Po)ρ + (ρ - ρo) (δ/δρ)(Aρρ)
A = + Aθ(Po)θ + (θ - θo) (δ/δθ)(Aθθ)
A = + Az(Po)z + (z - zo) (δ/δz)(Azz)
It provides the correct answer.
At this point, the rest of the analysis goes the same with both representations:
- The equation for A is developed, carrying out the derivatives, taking care since the unit vectors are not constant
- Collecting terms for each unit vector in the equation for A,
- The six elements for differential area, da is from :
- and six surface integrals are defined by taking the dot products and then evaluated
I could include more gory details in the double integrals. But, once the integrals are set up, I have gotten the same answer solving them manually and with a MAPLE tool (symbolic math calculations). Just hoping the error is in how this Taylor's Formula is applied. It seems that adding the extra terms is correct since the vector components are functions of all three cylindrical variables and the unit vectors are not constant, so not including them seems wrong when applying a directional derivative, but it isn't providing the correct answer. Thanks for any insight.
∇⋅A = Lim V→0 { ( ∫S A⋅da ) / V }
The vector field, A, is defined in cylindrical components such that:
A = Aρ(ρ,θ,z)ρ + Aθ(ρ,θ,z)θ + Az(ρ,θ,z)z
Where ρ, θ and z are the unit vectors in cylindrical coordinates, and Aρ, Aθ and Az are everywhere continuous and well defined functions.
The formula we are looking for (divergence in cylindrical coordinates):
∇⋅A = ( 1/ρ ) (δ/δρ) (ρAρ) + ( 1/ρ ) (δ/δθ)Aθ + (δ/δz)Az
I have found several similar analysis on-line, but most simply use the definition of the ∇ function in cylindrical coordinates and not Taylor's Formula. I am having a problem completing the analysis and it seems to stem from how Taylor's Formula is applied to the vector field. Hopefully the following is enough to convey the issue, I have lots more so that I could add if needed.
The vector field is represented by a Taylor's Series approximation about a point: Po(ρo,θo,zo)
At this point I would apply Taylor's Formula such that:
A = AAAρ(Po)ρ + (ρ - ρo) (δ/δρ)(Aρρ) + (θ - θo) (δ/δθ)(Aρρ) + (z - zo) (δ/δz)(Aρρ)
A = + Aθ(Po)θ + (ρ - ρo) (δ/δρ)(Aθθ) + (θ - θo) (δ/δθ)(Aθθ) + (z - zo) (δ/δz)(Aθθ)
A = + Az(Po)z + (ρ - ρo) (δ/δρ)(Azz) + (θ - θo) (δ/δθ)(Azz) + (z - zo) (δ/δz)(Azz)
Which almost provides the correct answer, but not quite:
( 1/ρ ) (δ/δρ) (ρAρ) + ( 1/ρ ) { (δ/δθ)Aθ + Aθ } + (δ/δz)Az
Notice the only difference is the Aθ term.
But if I apply Taylor's Formula like:
A = AAAρ(Po)ρ + (ρ - ρo) (δ/δρ)(Aρρ)
A = + Aθ(Po)θ + (θ - θo) (δ/δθ)(Aθθ)
A = + Az(Po)z + (z - zo) (δ/δz)(Azz)
It provides the correct answer.
At this point, the rest of the analysis goes the same with both representations:
- The equation for A is developed, carrying out the derivatives, taking care since the unit vectors are not constant
- Collecting terms for each unit vector in the equation for A,
- The six elements for differential area, da is from :
da ≡ (+/-)ρδθδzρ ; (+/-)δρδzθ ; (+/-)ρδρδθz
where plus is applied for the sides in the direction from Po of the unit vector, minus if in the other direction- and six surface integrals are defined by taking the dot products and then evaluated
I could include more gory details in the double integrals. But, once the integrals are set up, I have gotten the same answer solving them manually and with a MAPLE tool (symbolic math calculations). Just hoping the error is in how this Taylor's Formula is applied. It seems that adding the extra terms is correct since the vector components are functions of all three cylindrical variables and the unit vectors are not constant, so not including them seems wrong when applying a directional derivative, but it isn't providing the correct answer. Thanks for any insight.