James1238765
- 120
- 8
- TL;DR Summary
- What is the correct Christoffel numerical values for every point ##[x,y]## mapping a spherical surface to a plane surface?
The object takes a step [x, y] in 2 dimensional space. This is represented the change in coordinate ##x \vec e_x + y \vec e_y## where ##e_x## and ##e_y## are basis vectors in this space.
Suppose we define a non-linear / parametric transformation of this ##\vec e_x## and ##\vec e_y## basis vectors using 4 numbers defined all throughout the grid, specifying how each basis vector should transform into a second space.
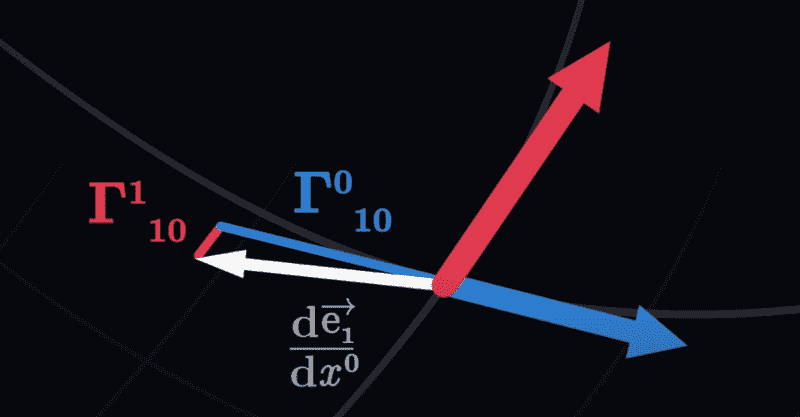
1. When the transform maps ##e_x \rightarrow e_{xprime}## and ##e_y \rightarrow e_{yprime}##, we get equivalent traced paths over time.

2. When the transform adds random noise between the basis vectors, we get:

What is the correct parametric specification of the individual numbers ##R_x^x, R_y^x, R_x^y, R_y^y## on this grid of four reals numbers ##[R_x^x, R_y^x, R_x^y, R_y^y]## defined explicitly on every grid point ##[x,y]##, that will trace the correct great circle path of a plane flying straight through the earth (geodesic line on a spherical surface)?
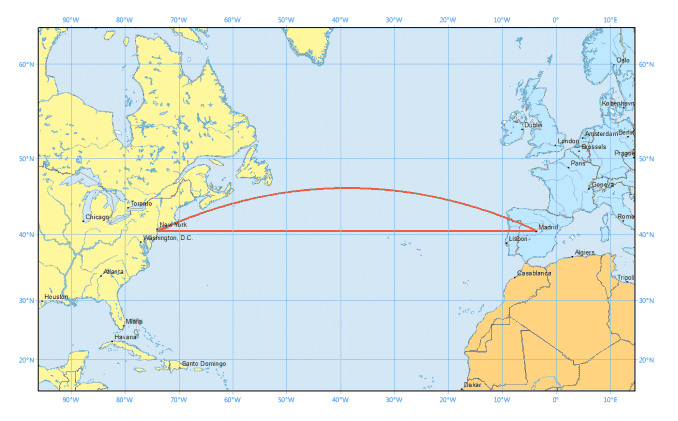
Suppose we define a non-linear / parametric transformation of this ##\vec e_x## and ##\vec e_y## basis vectors using 4 numbers defined all throughout the grid, specifying how each basis vector should transform into a second space.
1. When the transform maps ##e_x \rightarrow e_{xprime}## and ##e_y \rightarrow e_{yprime}##, we get equivalent traced paths over time.
2. When the transform adds random noise between the basis vectors, we get:
What is the correct parametric specification of the individual numbers ##R_x^x, R_y^x, R_x^y, R_y^y## on this grid of four reals numbers ##[R_x^x, R_y^x, R_x^y, R_y^y]## defined explicitly on every grid point ##[x,y]##, that will trace the correct great circle path of a plane flying straight through the earth (geodesic line on a spherical surface)?
