Geometric interpretations of double/triple integrals

[taylor__hasty]

I am currently taking calculus 3 and I am a little confused about the concept of double and triple integrals. Analytically, it's a breeze. I understand how to set limits, do all calculations, etc.

What my question is, when I get an answer, what does the answer "mean"? For example, in this problem:

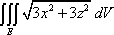
where E is the solid bounded by

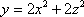
and the plane

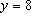
[FONT=Times New Roman, serif]Correct me if I'm wrong here, but I'll try to explain the way I understand. [/FONT]

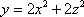
and y = 8 is the shape of the region that I'm integrating over. Let's say dV= dxdydz. Even if we removed the function under the integral, the shape of the region would remain the same. So what does the function represent geometrically? If we drop the function from the integral, we are left with the volume of the region described in the limits, correct? So what does the function tell us? And after integration, what does the result tell us?

Im really looking for a real world application of this stuff so I understand what exactly I am doing. Maybe in physics? When I asked my teacher, "what does the answer tell us/mean?" she responded "its the answer to the integral." Didn't really help.

Any help would be great. I am happy to be corrected! :)

 

[RUber]

One way to think of it is that the function is a density function. Then if you integrate the density over the volume, you will get a total mass contained within the volume.

 

[DEvens]

That particular integral does not have an obvious physical interpretation because there are no explanations for what the meaning of the various quantities are.

But sneak up on it like this. If instead of the square root in your integral you just had 1. That is obviously the volume. Suppose instead of 1 you had some constant K. Then you have K times the volume. That sounds a lot like the mass of an object of density K. Or possibly the total charge with charge density K. Or the total amount of a chemical with constant concentration K.

Now think about the square root. That looks a lot like a material with density a function of x and z given by the indicated square root. So this would be the mass of an object with this density as a function of x and z. Or the total amount of chemical if the concentration was given by that. It's kind of a strange function for a density. But suppose you had some kind of diffusion process that diffused in from large x and z values, but was uniform in y. Then it might produce a concentration like that. So this might be the total chemical if you then cut out the object described from a background material.

 

[taylor__hasty]

So the function is describing what is going on inside the shape that the limits define?

In a double integral, doesn't the function describe what is going on at the top of the region?

 

[RUber]

In a double integral, you are integrating over an area. Since people can visualize 3D, the function is often represented as a height and the double integral of a height function over the area of the region would return a volume.
Note that:
$\int_{x_1}^{x_2}\int_{y_1}^{y_2}\int_0^{f(x,y)} dz dy dx = \int_{x_1}^{x_2}\int_{y_1}^{y_2}f(x,y) dy dx$