Geometry and Trigonometry Challenge

[anemone]

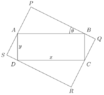
A rectangle with sides $x$ and $y$ is circumscribed by another rectangle of area $A^2$. Find all possible values of $A$ in terms of $x$ and $y$.

 

[Opalg]

[sp]Let $ABCD$ be the given rectangle and $PQRS$ a circumscribing rectangle, as in the diagram, where the angle $\theta = \angle PBA$ lies between $0$ and $\pi/2.$

View attachment 2700​

Then $PQ = PB+BQ = x\cos\theta + y\sin\theta$ and $PS = x\sin\theta + y\cos\theta$. So the area of $PQRS$ is $$A^2 = ( x\cos\theta + y\sin\theta)(x\sin\theta + y\cos\theta) = xy(\sin^2\theta + \cos^2\theta) + (x^2+y^2)\sin\theta\cos\theta = xy + \tfrac12(x^2+y^2)\sin2\theta.$$ Thus the minimum value of A^2 is $xy$ (when $\theta=0$ or $\pi/2$) and the maximum value is $xy + \frac12(x^2+y^2) = \frac12(x+y)^2$ (when $\theta = \pi/4$). Finally, $A$ takes all values from $\sqrt{xy}$ to $\frac1{\sqrt2}(x+y)$ inclusive.[/sp]

 

[anemone]

[sp]Let $ABCD$ be the given rectangle and $PQRS$ a circumscribing rectangle, as in the diagram, where the angle $\theta = \angle PBA$ lies between $0$ and $\pi/2.$

View attachment 2700​

Then $PQ = PB+BQ = x\cos\theta + y\sin\theta$ and $PS = x\sin\theta + y\cos\theta$. So the area of $PQRS$ is $$A^2 = ( x\cos\theta + y\sin\theta)(x\sin\theta + y\cos\theta) = xy(\sin^2\theta + \cos^2\theta) + (x^2+y^2)\sin\theta\cos\theta = xy + \tfrac12(x^2+y^2)\sin2\theta.$$ Thus the minimum value of A^2 is $xy$ (when $\theta=0$ or $\pi/2$) and the maximum value is $xy + \frac12(x^2+y^2) = \frac12(x+y)^2$ (when $\theta = \pi/4$). Finally, $A$ takes all values from $\sqrt{xy}$ to $\frac1{\sqrt2}(x+y)$ inclusive.[/sp]

Well done, Opalg and thanks for participating!:)