- #1
Chetlin
- 36
- 0
Geometry -- calculating a distance
I'm trying to calculate the distance from the center of one of these three tangent circles to the center of the entire shape (that is, the center of the "curvy triangular" region between the circles). Each circle has radius R. Here is a picture of the circles:
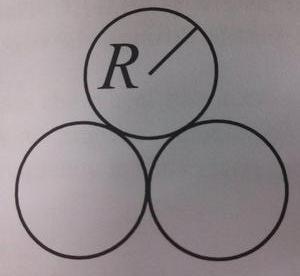
The distance is apparently [itex]R \sec 30^\circ[/itex] (equal to [itex]\frac{R}{\cos 30^\circ}[/itex]), which is [itex]\frac{2R}{\sqrt{3}}[/itex].
I guess the only one would be that [itex]\cos 30^\circ = \frac{\sqrt{3}}{2}[/itex].
I was able to solve it just fine by drawing a triangle, using the centers of the three circles as the angles, and drawing some more lines bisecting the angles (also splitting the opposing side into two equal halves), and then using properties of "30-60-90" triangles (which I guess is technically using sines and cosines) to figure out the same answer:
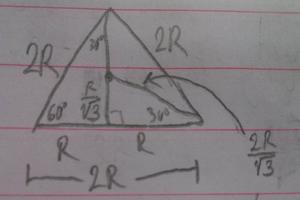
I don't understand, though, how you could see that the answer is [itex]R \sec 30^\circ[/itex] right away without doing all this. Am I able to realize this from the picture I made? I don't see how I could come up with that answer even after drawing the picture.
Homework Statement
I'm trying to calculate the distance from the center of one of these three tangent circles to the center of the entire shape (that is, the center of the "curvy triangular" region between the circles). Each circle has radius R. Here is a picture of the circles:
The distance is apparently [itex]R \sec 30^\circ[/itex] (equal to [itex]\frac{R}{\cos 30^\circ}[/itex]), which is [itex]\frac{2R}{\sqrt{3}}[/itex].
Homework Equations
I guess the only one would be that [itex]\cos 30^\circ = \frac{\sqrt{3}}{2}[/itex].
The Attempt at a Solution
I was able to solve it just fine by drawing a triangle, using the centers of the three circles as the angles, and drawing some more lines bisecting the angles (also splitting the opposing side into two equal halves), and then using properties of "30-60-90" triangles (which I guess is technically using sines and cosines) to figure out the same answer:
I don't understand, though, how you could see that the answer is [itex]R \sec 30^\circ[/itex] right away without doing all this. Am I able to realize this from the picture I made? I don't see how I could come up with that answer even after drawing the picture.