anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
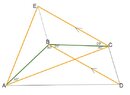
Let $ABCD$ be a convex quadrilateral such that $AB=BC,\,AC=BD,\,\angle CBD=20^{\circ},\,\angle ABD=80^{\circ}$. Find $\angle BCD.$