doomer
- 30
- 0
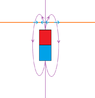
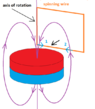
Magnetic field lines are loops, so at the surface of a magnet (axially magnetized) cylinder) pole they look like this? there is a dead zone at the center where there is no lines/magnetic field present?

or perhaps they look more like this? lines converge in the middle to a single line or point?
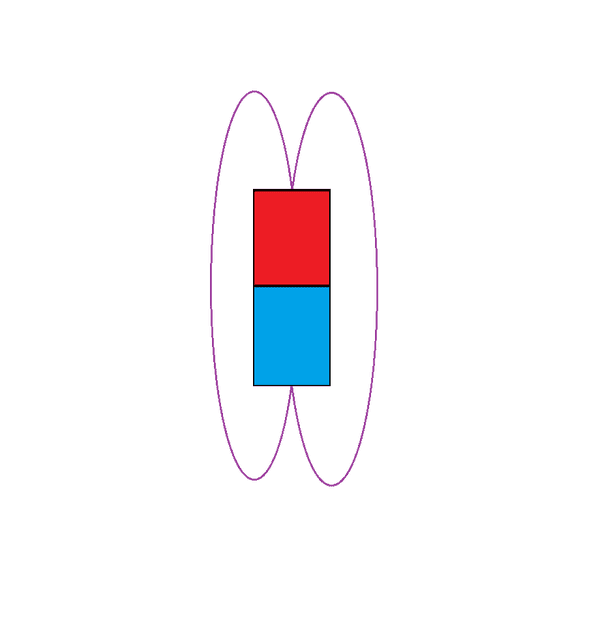
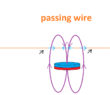
Which picture is correct? also on some googled pictures I can see a single straight line coming from the center of the pole that goes nowhere... I know that lines are really an mathematical artifact, I just want to know how the field is shaped near the surface at middle of the magnetic pole.
or perhaps they look more like this? lines converge in the middle to a single line or point?
Which picture is correct? also on some googled pictures I can see a single straight line coming from the center of the pole that goes nowhere... I know that lines are really an mathematical artifact, I just want to know how the field is shaped near the surface at middle of the magnetic pole.