Geometry of series terms of the Riemann Zeta Function

[Swamp Thing]

This is an Argand diagram showing the first 40,000 terms of the series form of the Riemann Zeta function, for the argument $\sigma + i t = 1/2 + 62854.13 \thinspace i$

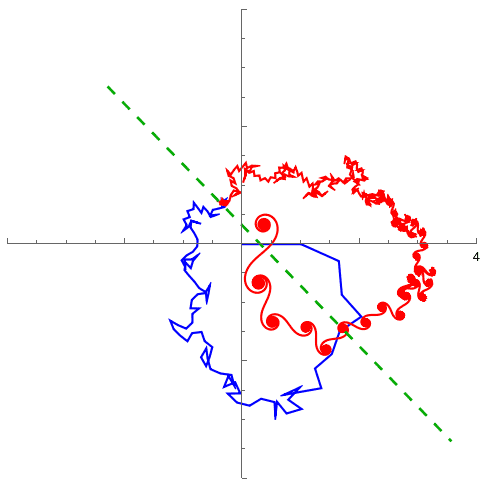
The blue lines are the first 100 (or so) terms, and the rest of the terms are in red. The plot shows a kind of approximate symmetry about the dotted green line, in the sense that the red part mirrors the blue part on average but is much more fine-grained. The last spiral in the red part is centred around the analytically continued value of zeta.

These aspects of the RZF seem rather interesting to me, but I could find only a limited amount of discussion about it --
1. https://arxiv.org/abs/1310.6396, G. Nickel, Geometry of the Riemann Zeta Function
2. https://arxiv.org/abs/1507.07631, G. Nickel. Symmetry in Partial Sums of the Riemann Zeta Function
3. https://ojs.stanford.edu/ojs/index.php/surj/issue/download/surj-2005/47, see pages 17-26.
4. http://laacademy.org/LAS2021/posters/P24_Conor_McGibboney.pdf

I am wondering why there isn't more interest in this. Is it because it is considered a dead end as far as research level mathematics?

Secondly, are there other sources that I have missed?

Thirdly, the symmetry property is not actually proved in the above references, but only explored phenomenologically. Is there a rigorous proof somewhere?

 

[martinbn]

...
I am wondering why there isn't more interest in this.
...

Shouldn't the question always be the opposite, why is there interest in this? What is the motivation?

 

[Swamp Thing]

Speaking only for myself -- curiosity.

It would make me happy to understand why the mirror symmetry emerges from this rather chaotic, almost Brownian behavior.

 

[Swamp Thing]

I decided to ask ChatGPT, mentioning the G. Nickel papers that I linked to in my OP.

ChatGPT:

As far as I know, the exact reason for the observed mirror symmetry in the partial sums of the Riemann zeta function has not been fully explained or proven. Nickel himself acknowledges this in his papers, stating that the symmetry is "striking" but that "its origins are not well understood".

Some researchers have proposed various explanations, such as the role of modular symmetry, the connection to the Selberg trace formula, and the connection to random matrix theory. However, these explanations are still speculative and there is no consensus on the exact reason for the observed symmetry. The phenomenon remains an active area of research in number theory and related fields.