Geometry problem midpoint theorem

[mathlearn]

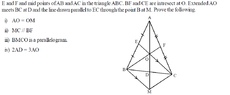
A problem on geometry proof

Hi (Smile),

View attachment 5807

When considering the $$\triangle$$ ABM E is the midpoint of AB
& EO //OM (given).I think this is the way to tell AO=OM , Help .Many Thanks (Smile)

 

[mrtwhs]

There are a lot of details to consider but the key fact needed is $$\triangle ODC \cong \triangle MDB$$ by SAA.

 

[mathlearn]

Many Thanks (Smile)

But I don't think there's a need to do so :)

I Think It has got something to do with

When considering the $$\triangle ABM$$ E is the midpoint of AB
& EO //OM (given)

Can you figure it out?Help.

Many Thanks (Smile)

 

[mrtwhs]

Many Thanks (Smile)

But I don't think there's a need to do so :)

I Think It has got something to do with

When considering the $$\triangle ABM$$ E is the midpoint of AB
& EO //OM (given)

Can you figure it out?Help.

Many Thanks (Smile)

I didn't mean to imply that my approach was the only way to do the problem. I just thought it would be straightforward. After you get the triangles I mentioned congruent, it is trivial that BMCO is a parallelogram and the rest of the problem follows.

The theorem that you are thinking of is a standard high school result:

In a plane, if a line goes through the midpoint of one side of a triangle and is parallel to a second side of the triangle, then it goes through the midpoint of the third side of the triangle.

 

[mathlearn]

A nice approach by saying the two triangles $$ODC \cong MBA$$ :)

By considering $$\triangle ABM$$

It is given that 'E' is the midpoint of AB. According to mrtwhs

"In a plane, if a line goes through the midpoint of one side of a triangle and is parallel to a second side of the triangle, then it goes through the midpoint of the third side of the triangle"

Line EO meets the side AM of the $$\triangle ABM$$

and it is also given that EC//BM $$\therefore EO//BM$$

And using the converse of the midpoint theorem

The straight line through the midpoint of one side of a triangle and parallel to another side,bisects the third side.

It can be proved that AO=OM;(Smile)

And can you help me tell that MC//BF and 2AD=3AO

Many Thanks :)

 

[Greg]

i) and ii) can be proved using the midpoint theorem. Using the fact that BM || EC and MC || BF, show that triangles BOC, BMC are congruent and triangles CMO and BMO are congruent. From that it follows that BMCO is a parallelogram (each diagonal of a parallelogram divides the parallelogram into two congruent triangles). To prove iv), use the fact that the diagonals of a parallelogram bisect each other.

 

[mathlearn]

Many Thanks :)

When considering the $$ \triangle AMC$$

O is the midpoint of AM (AO=OM)

F is the midpoint of AC (AF=FC)

The straight line through the midpoint of one side of a triangle and parallel to another side,bisects the third side.

$$\therefore OF//MC $$

$$\therefore MC//BF$$

And I now see

View attachment 5814

Help me to proceed

Many Thanks :)

 

[Evgeny.Makarov]

Concerning $2AD=3AO$: We have proved that $AO=OM$ and that $BMCO$ is a parallelogram. Diagonals in a parallelogram are divided in half; therefore, $OD=DM$. Thus, $2AD=2(AO+OD)=2(OM+OD)=2(2OD+OD)=6OD$ and $3AO=3OM=3\cdot2OD=6OD$.

 

[mathlearn]

Thank you very much ! (Smile)