Gergonne Point of Triangle ABC

[Painguy]

Hi there. This is my first post here so please excuse any mistakes i may make. I was going thur my textbook, and looking at various problems, and before I began my homework a certain problem caught my eye.
In the figure below the circle is tangent to the x-axis, to the y-axis, and to the line 3x+4=12

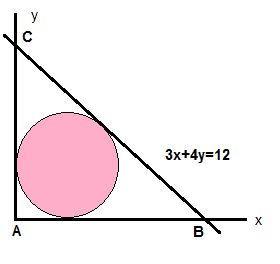a) Find the equation of the circle. Suggestion: decide the what the relationships must be between h, k, and r in the equation of a circle. Then find a way to apply it to the following formula: d = (|y0 -mx0-b|)/(sqrt(1+m^2))

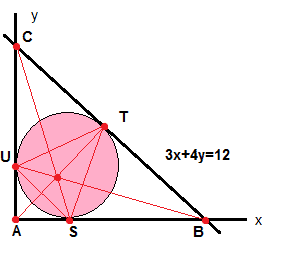
b) Let S, T, and U denote the points where the circle touches the x & y-axis & line 3x+4y=12. Find the equations through A and T; through B and U; through S and C

c) Where do the line segments AT and CS intersect? Where do AT and BU intersect.Here is what i have done.

point C is (0,3)
point B is (4,0)
point A is (0,0)

Where i get stuck is at part a. From my POV there is a lack of information making it impossible to continue, but that can't be the case.
I know that the equation of a circle is r^2=(x-h)^2+(y-k)^2 but how am stuck on how to find the solutions for the variables. I know that the point of origin for the circle isn't (0,0), but I am not rly given anything else to work with. Everything I have been asked of to do in this problem I can do, BUT only with a little bit more information. If I had the point of origin for the circle I wouldn't have a problem. I haven't even started my HW because of this problem. ITs bugging me soo much!

 

[Pi-Bond]

Since the circle is tangent to the two axes, the distance from both axes to the center of the circle is the same. Let this distance be a. Then the equation of the circle can be written as $(x-a)^2+(y-a)^2=a^2$ (mark your diagram to see this fact for yourself) You can use this to now find the value a from the tangent line.

 

[NascentOxygen]

If I had the point of origin for the circle I wouldn't have a problem.

The circle centre is at (r,r).

 

[Painguy]

------edit------
just to make sure i did step a correct can anyone check my work?
a)
$a= Ax+By+C/sqrt(A^2 + B^2)$

$a= Aa+Ba+C/sqrt(A^2 + B^2)$

$a= 3a+4a-12/sqrt(3^2 + 4^2)$

$a=(7a-12)/5$

$a=5(7a-12)$

$a=30/17=1.76?$

The book says that a=1 & the equation looks like this: $(x-1)^2+(y-1)^2=1$
but for now ill go with 1.8 until someone corrects me.
for part b i can find BU, SC, but not AT

b)
BU: $y-y1=m(x-x1)$

$y-1.8=(1-0/0-4)(x-0)$

$y=-1x/4+1$

SC: $y-y1=m(x-x1)$

$y-3=(3-0/1.8)(x-0)$

$y=-3x/1.8+3$

AT:?

for part c i plan to set the lines equal to each other for y to get x and the other way around, but because i can't figure out AT i will wait.

 

[NascentOxygen]

The book says that a=1 & the equation looks like this: (x-1)^2+(y-1)^2=1

The book is correct.

If radius=1.8 then that would make the height of the circle 3.6, yet at point C the tangent intersects the y-axis at y=3 and the circle must fit well underneath this line. Hence impossible.

 

[Painguy]

The book is correct.

If radius=1.8 then that would make the height of the circle 3.6, yet at point C the tangent intersects the y-axis at y=3 and the circle must fit well underneath this line. Hence impossible.

i see. well i just noticed where i made my mistake. a=5(7a-12)...can't do that -__-
$a=(7a-12)/5$

$5a=7a-12$

$-2a=-12$

$a=6$

a=6? but that also cannot workout. sooooo...how does the book get that equation? I am probably overlooking something obvious here, but as u can notice i tend to do that

 

[Pi-Bond]

Your formula has an absolute value, so there would be two cases, i.e. when 7a-12>0 and when 7a-12<0. There will thus be two circles whose center is (a,a) and have radius a, but only one will be tangent to both axes as well.

 

[Painguy]

Your formula has an absolute value, so there would be two cases, i.e. when 7a-12>0 and when 7a-12<0. There will thus be two circles whose center is (a,a) and have radius a, but only one will be tangent to both axes as well.

what did u do to the 1/5? It was (7a-12)/5 :/ sry to protest, but something doesn't seem right there.

 

[NascentOxygen]

I didn't follow what the Suggestion was about. So I solved this problem my way.

We know the equation of the tangent. At the point of tangency, the normal to the tangent has a slope of 4/3 and it passes through the centre of the circle (a,a). So the x ordinate at the point of tangency is a+3a/5 and this point being on the tangent we find y.

We know the distance from (a,a) to the point of tangency equals the radius, and this gives us a quadratic in a. Solve for the possible values of the radius.

 

[Pi-Bond]

The 1/5 is there, I was only talking about the part in the absolute value. Your equation is then

$a=\frac{|7a-12|}{5}$

There are two solutions to this equations; you have already found the one where a=6 (the case when 7a-12>0). You need to now consider the other case, i.e. when 7a-12<0.