- #1
student93
- 85
- 0
Homework Statement
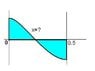
Problem is attached in this post.
Homework Equations
Problem is attached in this post.
The Attempt at a Solution
I set my Integral as ∫cos2π dx from 0 to 1/2 and get an answer of 0, which is incorrect.
The correct answer is 1/π, but I don't understand why etc.