Gibbs adsorption isotherm derivation

[ussername]

Let's consider an isotherm isobaric adsorption of gas (A) on the adsorbent (B). There are two phases in the system:
- volume phase (1) that consists of gas and adsorbent.
- surface phase (2) that contains a layer of adsorbed gas on the surface of adsorbent.

When deriving Gibbs adsorption isotherm, the work needed to change the surface of interface of phase (1) is neglected, i.e. the Gibbs free energy changes for both phases are:

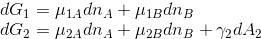
I wonder why one can neglect

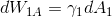? During adsorption the gas passes from phase (1) into phase (2) and the surface of interface of (1) is changing. Why is that?

 

[TeethWhitener]

First, are you sure the surface area term isn't supposed to be $A_2d\gamma_2$?

To answer your question, writing out the total Gibbs free energy $G = G_1+G_2$ gives
$$G = U_1 + U_2 +P_1V_1 - T_1S_1-T_2S_2 +\mu_{1A}N_A +\mu_{1B}N_B +\mu_{2A}N_A +\mu_{2B}N_B + \gamma A$$
(NB--the $P_2V_2$ term disappears because I'm assuming the surface has zero volume) (also, sorry in advance if I mess this up: I'm used to working with an interface and two bulk phases, not one bulk phase). Since there's only one surface (the surface of phase 1 and the surface of phase 2 are the same surface), we only have a single $\gamma A$ term, not one for each phase. If we want to divide the Gibbs free energy terms into one part for the bulk and one part for the surface, it doesn't really make much sense to put the surface tension work term into the bulk Gibbs energy. So it ends up in the surface free energy expression.

 

[ussername]

Thank you for your answer, but first of all I need to clarify where can be Gibbs adsorption isotherm used.
If it would be applied to a solid adsorbent - what is the meaning of surface tension? It is the surface tension when changing the surface of the solid adsorbent? If so, I have no idea how one can measure it. I know only measuring techniques to determine surface tension of liquids.

 

[TeethWhitener]

$\gamma A$ is the work done to form the interface. In a liquid-liquid system or a liquid-gas system, we equate $\gamma$ with surface tension, but in general it represents surface energy density per unit area. There are a few different ways to measure this, the most straightforward of which is probably contact angle measurements.

 

[ussername]

I wonder why one can neglect

?

I think a good explanation is that in gaseous phase the surface work is negligible due to weak intermolecular attraction forces.
In such case I'm nearly able to derive Gibbs adsorption isotherm.
During isotherm isobaric process (neglecting surface works in both phases) the equilibrium criteria is the Gibbs energy minimum:
G(n_A,n_B)=min
Also that is:
μ_1A=μ_2A
μ_1B=μ_2B

But, how can I derive that even differential forms of chemical potencials are equal (dμ_1A=dμ_2A, dμ_1B=dμ_2B) in equilibrium?

 

[TeethWhitener]

μ1A=μ2A
μ1B=μ2B

But, how can I derive that even differential forms of chemical potencials are equal (dμ1A=dμ2A, dμ1B=dμ2B) in equilibrium?

Just substitute $\mu_{1A}$ for $\mu_{2A}$ before taking the exterior derivative.

 

[TeethWhitener]

I think a good explanation is that in gaseous phase the surface work is negligible due to weak intermolecular attraction forces.

Again, you're only making one interface. If you include two $\gamma A$ terms, you overcount. It's like saying that you're creating a gas-solid interface as well as a solid-gas interface. It's the same interface.

 

[ussername]

If you include two γA terms, you overcount

I don't think so. I consider two subsystems (bulk and surface). For each of them I can express the Gibbs energy total differential and for each of them I perform a surface work when moving a particle to the interface (and those surface works generally differ).

Just substitute $\mu_{1A}$ for $\mu_{2A}$ before taking the exterior derivative.

It seems better for me to derive it from the equality of mixed derivatives of Gibbs energy with its total differential:
dG=μ_A1⋅dn_A1+μ_B1⋅dn_B1+μ_A2⋅dn_A2+μ_B2⋅dn_B2
That is:

From that the differential forms of chemical potencials are opposite but I suppose it does not matter.

 

[TeethWhitener]

For each of them I can express the Gibbs energy total differential and for each of them I perform a surface work when moving a particle to the interface (and those surface works generally differ).

But the surface is the interface. I'm not sure how I can explain this more clearly.