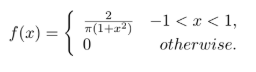sofanglom
- 1
- 0
Hi :) Here's my problem along with what I've done.
Here is the problem:
View attachment 8716
That is the p.d.f. of a random variable X.
I have to find the cdf. I don't know which I should do so I tried it two ways. First:
$\int_{-1}^{1} \ \frac{2}{\pi(1+x^{2})} dx = {{\frac{2}{\pi} arctan(x)]}^{1}}_{-1}=1$
Second:
$\int_{-1}^{x} \ \frac{2}{\pi(1+t^{2})} dt = {{\frac{2}{\pi} arctan(x)]}^{x}}_{-1}=\frac{2(arctan(x)+\frac{\pi}{4}}{\pi}$
Which one is the required CDF for X?
Here is the problem:
View attachment 8716
That is the p.d.f. of a random variable X.
I have to find the cdf. I don't know which I should do so I tried it two ways. First:
$\int_{-1}^{1} \ \frac{2}{\pi(1+x^{2})} dx = {{\frac{2}{\pi} arctan(x)]}^{1}}_{-1}=1$
Second:
$\int_{-1}^{x} \ \frac{2}{\pi(1+t^{2})} dt = {{\frac{2}{\pi} arctan(x)]}^{x}}_{-1}=\frac{2(arctan(x)+\frac{\pi}{4}}{\pi}$
Which one is the required CDF for X?