- #1
fab13
- 318
- 6
In the context of a project, I had to solve numerically Poisson equation with cylindrical coordinates. I put here results for z = 0 on a 3D mesh 256x256x256.
Below 1 figure representing the final solution (in absolute value) in the case of a galaxy; I use the CGS units for the potential.
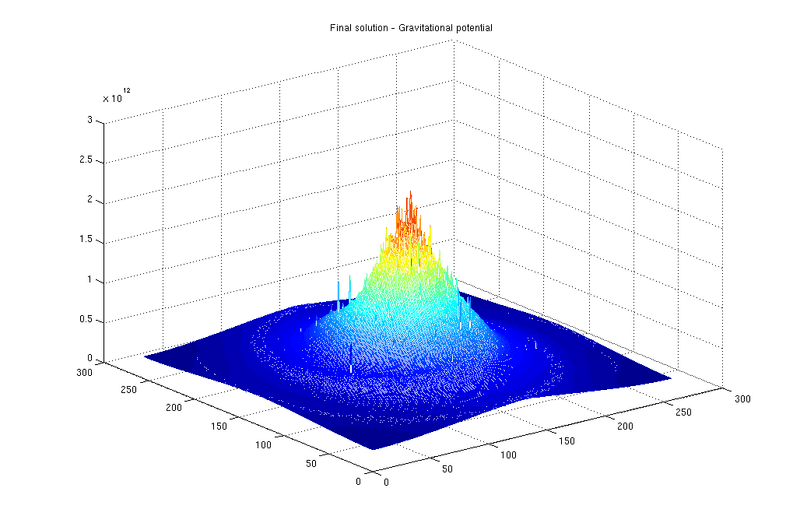
I have 2 questions :
1*) I would like to know if the values that I get are valid with a similar real galaxy.
The characteristic features of this galaxy are : there are 10240 stars (each has 1 solar mass), the radius is equal to 25 kiloparsec (including arms).
A simple computation is done with the following formula :
abs(Phi(r)) = ∑ -Gm/(r-r(i))
For example, taking the positions of all the stars (10240 stars), I get for the potential at r = 1 kpc :
abs(Phi(1)) = 2.1 * 10^9 cm^2 s^-2
As you can see, I don't succeed to get the same value : look at near the center, I get approximately 2.5 10^12 cm^2 s^-2 : the difference is about 10^3, that's high.
Anyone could tell me why I don't get the same value for this radius ( r= 1 kpc) ?
In my code, I solve Poisson equation with discrete Fourier transform. Firstly, I compute the matter distribution (rho in Poisson equation) and after, the green function.
Here the code snippet for density (with space_x, space_y, space_y the size of a cell in grid, expressed in kiloparsec) :
Here the code snippet for green function (with Ng=256 in my case) :
2*) When I define Green function, have I to add a factor space_x, space_y and space_z respectively for dx, dy, dz ? I mean like this below :
If I don't add these factors, i.e :
I get the following result :
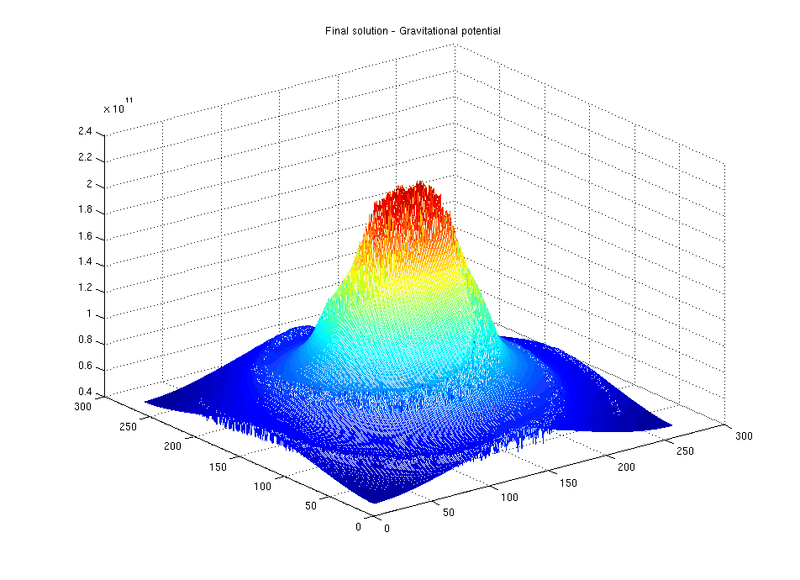
As you can see, the potential is more smoothed around the center. So I don't know if I have to include or not these space_x, space_y and space_z in Green function.
From your experience and the characteristics of this galaxy (number of stars equal to 10240, solar mass for each star and radius about 25 kpc), which figure seems to be valid ? the first image or the second ?
Any help is welcome
Below 1 figure representing the final solution (in absolute value) in the case of a galaxy; I use the CGS units for the potential.
I have 2 questions :
1*) I would like to know if the values that I get are valid with a similar real galaxy.
The characteristic features of this galaxy are : there are 10240 stars (each has 1 solar mass), the radius is equal to 25 kiloparsec (including arms).
A simple computation is done with the following formula :
abs(Phi(r)) = ∑ -Gm/(r-r(i))
For example, taking the positions of all the stars (10240 stars), I get for the potential at r = 1 kpc :
abs(Phi(1)) = 2.1 * 10^9 cm^2 s^-2
As you can see, I don't succeed to get the same value : look at near the center, I get approximately 2.5 10^12 cm^2 s^-2 : the difference is about 10^3, that's high.
Anyone could tell me why I don't get the same value for this radius ( r= 1 kpc) ?
In my code, I solve Poisson equation with discrete Fourier transform. Firstly, I compute the matter distribution (rho in Poisson equation) and after, the green function.
Here the code snippet for density (with space_x, space_y, space_y the size of a cell in grid, expressed in kiloparsec) :
Code:
for (i=0; i< Ng; i++)
{
for (j=0; j< Ng; j++)
{
for (k=0; k< Ng; k++)
{
compute(i, j, k, node_x, node_y, node_z); // Compute the coordinates of cell on the grid
density[node_x][node_y][node_z] = density[node_x][node_y][node_z] + mass/((space_x*space_y*space_z));
}
}
}
Code:
for (i=0; i< Ng; i++)
{
for (j=0; j< Ng; j++)
{
for (k=0; k< Ng; k++)
{
compute(i, j, k, node_x, node_y, node_z); // Compute the coordinates of cell on the grid
density[node_x][node_y][node_z] = density[node_x][node_y][node_z] + mass/((space_x*space_y*space_z));
}
}
}2*) When I define Green function, have I to add a factor space_x, space_y and space_z respectively for dx, dy, dz ? I mean like this below :
Code:
for (i=0; i< Ng; i++)
{
for (j=0; j< Ng; j++)
{
for (k=0; k< Ng; k++)
{
compute(i, j, k, node_x, node_y, node_z); // Compute the coordinates of cell on the grid
density[node_x][node_y][node_z] = density[node_x][node_y][node_z] + mass/((space_x*space_y*space_z));
}
}
}If I don't add these factors, i.e :
Code:
for (i=0; i< Ng; i++)
{
for (j=0; j< Ng; j++)
{
for (k=0; k< Ng; k++)
{
compute(i, j, k, node_x, node_y, node_z); // Compute the coordinates of cell on the grid
density[node_x][node_y][node_z] = density[node_x][node_y][node_z] + mass/((space_x*space_y*space_z));
}
}
}I get the following result :
As you can see, the potential is more smoothed around the center. So I don't know if I have to include or not these space_x, space_y and space_z in Green function.
From your experience and the characteristics of this galaxy (number of stars equal to 10240, solar mass for each star and radius about 25 kpc), which figure seems to be valid ? the first image or the second ?
Any help is welcome
Last edited: