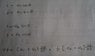- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Understanding the Reciprocal Form of Sin and Cos in Polar Coordinates
- Thread starter athrun200
- Start date
-
- Tags
- Coordinate Gradient Polar
In summary, you seem to understand how to do multivariate calculus, but you make a mistake when you switch coordinates from cartesian to polar. You also need to switch the unit vectors from cartesian to polar. If you correct these mistakes, you'll get the correct answer.
Physics news on Phys.org
- #2
I like Serena
Homework Helper
MHB
- 16,336
- 258
Hi athrun200! 
You seem to understand how to do multivariate calculus.
I didn't check all your equations, but they seem right.
However, you end up in an expression with i and j, when you should be ending up in an expression with [itex]\boldsymbol{e_{r}}[/itex] and [itex]\boldsymbol{e_{\theta}}[/itex].
Perhaps you should make a substitution like that?
You seem to understand how to do multivariate calculus.
I didn't check all your equations, but they seem right.
However, you end up in an expression with i and j, when you should be ending up in an expression with [itex]\boldsymbol{e_{r}}[/itex] and [itex]\boldsymbol{e_{\theta}}[/itex].
Perhaps you should make a substitution like that?
- #3
athrun200
- 277
- 0
In fact, the first term on my last step is very similar to [itex]\boldsymbol{e_{r}}[/itex] and same for the second term. Can I really convert them to [itex]\boldsymbol{e_{\theta}}[/itex] by substitution ?I like Serena said:However, you end up in an expression with i and j, when you should be ending up in an expression with [itex]\boldsymbol{e_{r}}[/itex] and [itex]\boldsymbol{e_{\theta}}[/itex].
Perhaps you should make a substitution like that?
Sorry that I can't think of any substitution which is useful.
- #4
I like Serena
Homework Helper
MHB
- 16,336
- 258
You're making a transition from cartesian coordinates to polar coordinates.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.Edit: I just checked a little bit of your equations, and I do not understand how you got [itex]\frac {\partial r} {\partial x} = \frac 1 {\cos \theta}[/itex].
That looks wrong.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.Edit: I just checked a little bit of your equations, and I do not understand how you got [itex]\frac {\partial r} {\partial x} = \frac 1 {\cos \theta}[/itex].
That looks wrong.
- #5
- #6
athrun200
- 277
- 0
I like Serena said:You're making a transition from cartesian coordinates to polar coordinates.
In your relevant equations section you have defined the relation between the unit vectors of the two sets of coordinates.
What you need is the inverse relation.
And in your attempt you switch the coordinates from cartesian to polar, which is good, but you also need to switch the unit vectors from cartesian to polar.
Edit: I just checked a little bit of your equations, and I do not understand how you got [itex]\frac {\partial r} {\partial x} = \frac 1 {\cos \theta}[/itex].
That looks wrong.
I obtain it like this. (I am also not sure about it.)
Attachments
- #7
I like Serena
Homework Helper
MHB
- 16,336
- 258
Ah well, that is not right.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have to differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in [itex]r = \sqrt{x^2+y^2}[/itex], take the derivative, and simplify any way you like afterward.
You'll get a different result for [itex]\frac {\partial r} {\partial x}[/itex] then, which is also why your end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have to differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in [itex]r = \sqrt{x^2+y^2}[/itex], take the derivative, and simplify any way you like afterward.
You'll get a different result for [itex]\frac {\partial r} {\partial x}[/itex] then, which is also why your end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
Last edited:
- #8
athrun200
- 277
- 0
I get the answer! Thx!I like Serena said:Ah well, that is not right.
If you take the partial derivative on the right side, you need to apply the product rule, meaning you also have the differentiate theta.
If you do that, you'll not find it so easy to calculate dr/dx.
Instead I suggest you fill in [itex]r = \sqrt{x^2+y^2}[/itex], take the derivative, and simplify any way you like afterward.
You'll get a different result for [itex]\frac {\partial r} {\partial x}[/itex] then, which is also why you're end result is off by a factor 2.
If you correct this and the similar mistakes, you'll find the proper end result.
- #9
I like Serena
Homework Helper
MHB
- 16,336
- 258
Good! And thanks for your thx. 
FAQ: Understanding the Reciprocal Form of Sin and Cos in Polar Coordinates
1. What is the formula for finding the gradient in polar coordinates?
The formula for finding the gradient in polar coordinates is ∇f = (∂f/∂r)er + (1/r)(∂f/∂θ)eθ, where r is the radial coordinate and θ is the angular coordinate.
2. How does the gradient change in polar coordinates compared to Cartesian coordinates?
In polar coordinates, the gradient is expressed in terms of the radial and angular coordinates, while in Cartesian coordinates it is expressed in terms of the x and y coordinates. Additionally, the gradient in polar coordinates includes a factor of 1/r, which reflects the change in distance from the origin.
3. What does the magnitude of the gradient represent in polar coordinates?
The magnitude of the gradient in polar coordinates represents the slope of the function in the direction of the gradient vector. This can be thought of as the rate of change of the function with respect to distance and direction from the origin.
4. Can the gradient be negative in polar coordinates?
Yes, the gradient can be negative in polar coordinates. This indicates that the function is decreasing in the direction of the gradient vector. However, the magnitude of the gradient will always be positive.
5. How can I use the gradient in polar coordinates to find the direction of steepest increase?
The direction of steepest increase is given by the direction of the gradient vector. In polar coordinates, this can be found by taking the arctan of (∂f/∂θ)/(∂f/∂r). This will give the angle at which the function has the greatest increase.
Similar threads
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 3
- Views
- 535
- Replies
- 14
- Views
- 3K
- Replies
- 22
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 3
- Views
- 1K
Share: