chowdhury
- 34
- 3
- TL;DR Summary
- Algebraic manipulation
How to write following equation in index notation?
$$\nabla \cdot \left( \mathbf{e} : \nabla_{s} \mathbf{u} \right)$$
where ##e## is a third rank tensor, ##u## is a vector, ##\nabla_{s}## is the symmetric part of the gradient operator, : is the double dot product.
The way I approached is
$$\mathbf{e} : \nabla_{s} \mathbf{u} = e_{iJ} \nabla_{Jk} u_{k}$$, where i = x,y,z, and J = 1,2,3,4,5,6
$$\nabla \cdot \left( \mathbf{e} : \nabla_{s} \mathbf{u} \right) = \nabla_{i} e_{iJ} \nabla_{Jk} u_{k} = \frac{\partial e_{iJ}}{\partial r_{i}} \nabla_{Jk} u_{k} = e_{iJ} \nabla_{i} \nabla_{Jk} u_{k} = e_{iJ} \nabla_{i} u_{k, \color{red}{kJ}} = e_{iJ} u_{k, \color{red}{ikJ}} $$
But in the book it is written as
$$ \nabla_{i} e_{iL} \nabla_{Lj} u_{j} = \color{red}{e_{ikj} u_{j, ik}}$$
I am from the book, B. A. Auld, Acoustic fields and waves in solids, vol. 1, 1973.
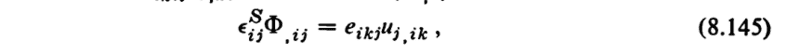
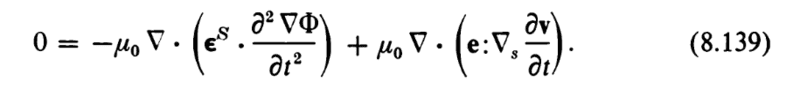

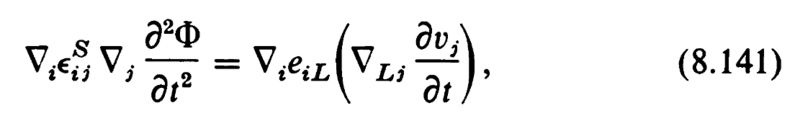
$$\nabla \cdot \left( \mathbf{e} : \nabla_{s} \mathbf{u} \right)$$
where ##e## is a third rank tensor, ##u## is a vector, ##\nabla_{s}## is the symmetric part of the gradient operator, : is the double dot product.
The way I approached is
$$\mathbf{e} : \nabla_{s} \mathbf{u} = e_{iJ} \nabla_{Jk} u_{k}$$, where i = x,y,z, and J = 1,2,3,4,5,6
$$\nabla \cdot \left( \mathbf{e} : \nabla_{s} \mathbf{u} \right) = \nabla_{i} e_{iJ} \nabla_{Jk} u_{k} = \frac{\partial e_{iJ}}{\partial r_{i}} \nabla_{Jk} u_{k} = e_{iJ} \nabla_{i} \nabla_{Jk} u_{k} = e_{iJ} \nabla_{i} u_{k, \color{red}{kJ}} = e_{iJ} u_{k, \color{red}{ikJ}} $$
But in the book it is written as
$$ \nabla_{i} e_{iL} \nabla_{Lj} u_{j} = \color{red}{e_{ikj} u_{j, ik}}$$
I am from the book, B. A. Auld, Acoustic fields and waves in solids, vol. 1, 1973.
Last edited: