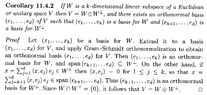Gram-Schmidt Orthonormalization .... Garling, Corollary 11.4.2 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help to fully understand the proof of Corollary 11.4.2 ...Garling's statement and proof of Corollary 11.4.2 reads as follows:View attachment 8971In the third sentence of the above proof by Garling we read that:

$$\text{span}( e_{k + 1}, \ ... \ ... , e_d ) \subseteq W^{ \bot }$$ Although this claim looks very plausible I am unable to formulate a rigorous demonstration of its truth ...

Can someone provide a rigorous argument showing that $$\text{span}( e_{k + 1}, \ ... \ ... , e_d ) \subseteq W^{ \bot }$$ ... ... ?
Help will be appreciated ...

Peter
==========================================================================================

Since I suspect a rigorous proof of the above claim of interest will involve Theorem 11.4.1 ( Gram-Schmidt Orthonormalization ... ) ... I am providing text of the same ... as follows:
View attachment 8972
View attachment 8973
Hope that helps ...

Peter

 

[Opalg]

Can someone provide a rigorous argument showing that $$\text{span}( e_{k + 1}, \ ... \ ... , e_d ) \subseteq W^{ \bot }$$ ... ... ?
Peter

If $1\leqslant i\leqslant k$ and $k+1\leqslant j\leqslant d$ then $\langle e_i,e_j\rangle = 0$. So $e_j$ is orthogonal to each member of the orthonormal basis of $W$, and therefore orthogonal to everything in $W$. In other words, $e_j\in W^\bot$. Since that holds for all $j$ with $k+1\leqslant j \leqslant d$, it follows that $\text{span}(e_{k+1},\ldots,e_d) \subseteq W^\bot$.

 

[Math Amateur]

If $1\leqslant i\leqslant k$ and $k+1\leqslant j\leqslant d$ then $\langle e_i,e_j\rangle = 0$. So $e_j$ is orthogonal to each member of the orthonormal basis of $W$, and therefore orthogonal to everything in $W$. In other words, $e_j\in W^\bot$. Since that holds for all $j$ with $k+1\leqslant j \leqslant d$, it follows that $\text{span}(e_{k+1},\ldots,e_d) \subseteq W^\bot$.

Thanks for the help, Opalg ...

Much appreciated!

Peter