Graph Reading: Get it Right the First Time!

[knapklara]

Homework Statement

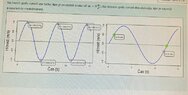
Velocity graph, find where acceleration is zero and where acceleration is maximum.

Relevant Equations

We have two graphs with velocity and time. On the first one, I have to find all the points, where acceleration is zero.
On the second picture I need to find 2 points where acceleration is maximum.

I'm fairly certain that the first one is marked correctly.
Should the second one be where there are red marks or is it correct as it was marked previously? Any advice with graph reading?

 

[malawi_glenn]

The acceleration is maximal where the absolute value of the slope is maximal.

 

[hmmm27]

What makes you think the notations on the first graph are correct ? and, what makes you think the ones on the second graph are incorrect... and that yours are correct.

If it helps, they're both (probably) supposed to be sine waves, but that shouldn't matter.

 

[Steve4Physics]

Say you have a graph of velocity vs. time.
P is some point on the graph.
You draw (or imagine) the tangent at P.

Question: How can you tell the accelerastion at P from the tangent's direction?

 

[knapklara]

I appreciate your feedback but I'm afraid it's too complicated for me.
Pic 1
Where there's velocity increasing, I would say that there's acceleration and just before the velocity starts decreasing, I'd say acceleration is zero, that's also where it is marked.
Pic 2
Since the object starts moving from 0, I'd say the acceleration is then the biggest, isn't it so?

I don't want to sound rude or ungrateful for your help but my field of studies is physiotherapy and I really don't want to go into too much detail. This is an actual example of a task at an exam, even though the task might be simplified.

 

[malawi_glenn]

There is always acceleration when then velocity is changing.

 

[knapklara]

There is always acceleration when then velocity is changing.

So where would acceleration be zero or close to zero then reading the first graph?

 

[malawi_glenn]

So where would acceleration be zero or close to zero then reading the first graph?

Do you know how position-time graphs work?
Acceleration-time graphs works quite similar as those.

 

[knapklara]

Do you know how position-time graphs work?
Acceleration-time graphs works quite similar as those.

I know how to read the basics from a graph such as what's the velocity at x time and so on... What do you mean exactly by how those graphs work?

 

[Steve4Physics]

Hi @knapklara. The rules here prevent us from telling you the answers directly. This is in your own interest!

If you have a velocity-time graph, the ‘steepness’ of each part of the graph tells you the acceleration.

a) If a part of the graph is uphill and steep, that means a large positive value for acceleration (because it shows velocity is increasing quickly).

b) If a part of the graph is downhill and steep, that means a large negative value for acceleration (because it shows velocity is decreasing quickly).

c) If a part of the graph is flat (horizontal), that means zero acceleration (because the ‘flatness’ shows the velocity is not changing).

Look at your 2nd graph (the one with the red marks).

Is the first red mark an a), b) or c)?
Is the second red mark an a), b) or c)?

 

[malawi_glenn]

I know how to read the basics from a graph such as what's the velocity at x time and so on... What do you mean exactly by how those graphs work?

In a position-time graph, how do you find points where the speed is zero, and how do you find points where the speed is maximum?

 

[Delta2]

In general if you have the graph of f(x), then the points where the tangent to the graph becomes parallel to the x-axis are the points where f'(x)=0, and the points where the tangent to the graph becomes vertical to the x-axis are the points where f'(x)=maximum.

Actually the maximum points for f'(x) are the points of the graph of f(x) where the tangent to the point of the graph becomes as more vertical (to the x-axis) as we can get. They might be not exactly vertical.

 

[knapklara]

Hi @knapklara. The rules here prevent us from telling you the answers directly. This is in your own interest!

If you have a velocity-time graph, the ‘steepness’ of each part of the graph tells you the acceleration.

a) If a part of the graph is uphill and steep, that means a large positive value for acceleration (because it shows velocity is increasing quickly).

b) If a part of the graph is downhill and steep, that means a large negative value for acceleration (because it shows velocity is decreasing quickly).

c) If a part of the graph is flat (horizontal), that means zero acceleration (because the ‘flatness’ shows the velocity is not changing).

Look at your 2nd graph (the one with the red marks).

Is the first red mark an a), b) or c)?
Is the second red mark an a), b) or c)?

Thank you very much for your explanation, you explained it wonderfully for someone who is not too much of a "physicist".
Now I would say that the second graph is also done correctly as it is, without my red marks.
It confused me a little because I was looking at a graph of a sprinter and there the maximum acceleration is at the beginning and then the acceleration goes to zero and then negative acceleration after reaching top speed.

 

[knapklara]

Or I'd maybe even put it like this based on your explanation. Is it correct that maximum velocity is then found in the middle of the steep, did I get that right?

 

[malawi_glenn]

Now I would say that the second graph is also done correctly as it is, without my red marks.

Only one of these points are correct

trace the curve with a ruler, which is held tangent to the curve. Find the point where the ruler is point up or down the most: https://giphy.com/embed/height=400;id=lvXRxRBiFDpYY;type=gif;width=400

 

[hmmm27]

The steepest points on a vt graph are the maximal acceleration.

Now I would say that the second graph is also done correctly as it is, without my red marks.

Given that the question doesn't specify the function or dataset that produced the graph(s), your eyeballing isn't too bad - it does look like the predefined points could be right.

Is it correct that maximum velocity is then found in the middle of the steep, did I get that right?

Based on the assumption that those are supposed to be sine waves, the zero-crossings are the maxima, ie: if your "steep" encompasses both + and -, then yes.

[edit: also based on you meaning to say "maximum acceleration" instead of "maximum velocity", thanks @Steve4Physics]

Note that, for simplicity's sake, the beginning of the graph doesn't actually cross zero.

Now, about my ankle...

 

[Steve4Physics]

Or I'd maybe even put it like this based on your explanation. Is it correct that maximum velocity is then found in the middle of the steep, did I get that right?

No. Maybe you are confusing distance-time graphs and velocity-time graphs. Care is needed!

For a distance-time graph, the biggest velocity is where the graph is steepest (maximum gradient). But the question gives a velocity-time graph!

For a velocity-time graph, the biggest velocity is simply the highest point on the graph. (The biggest acceleration is where the graph is steepest (maximum gradient).)

Also note, to find the point(s) with zero acceleration on a velocity-time graph, you find where the graph is flat (horizontal). The graph is flat at the very top of a ‘hill’ on the graph, or at the very bottom of a ‘valley’ on the graph.