zenterix
- 774
- 84
- TL;DR Summary
- We can obtain equations relating ##P## and ##V## for both an isothermal and adiabatic quasi-static processes for an ideal gas. In a PVT diagram, we can plot equilibrium points for such processes. But in the case of the adiabatic process, how do we know how ##T## varies as we vary ##P## and ##V##?
Let me first get through a few calculations to set up the main part of this question.
From the first law, we have that
$$dQ = dU - dW\tag{1}$$
Now, we also have
$$dU=\left (\frac{\partial U}{\partial T} \right )_VdT + \left (\frac{\partial U}{\partial V} \right )_T dV\tag{2}$$
$$dW=-PdV\tag{3}$$
and so
$$dQ = \left (\frac{\partial U}{\partial T} \right )_VdT + \left (\frac{\partial U}{\partial V} \right )_T dV +PdV\tag{4}$$
$$=\left (\frac{\partial U}{\partial T} \right )_VdT +\left ( \left (\frac{\partial U}{\partial V} \right )_T + P \right )dV\tag{5}$$
If we consider ##V## constant, then
$$C_V=\left (\frac{dQ}{dT}\right )_V=\left (\frac{\partial U}{\partial T} \right )_V\tag{6}$$
That is, we reach an equation for the constant volume heat capacity. For some temperature change, the amount of heat equals the change in internal energy.
Therefore, from (1) we have
$$dQ=dU-dW=C_V+PdV\tag{7}$$
Since we have an ideal gas, we also know that any equilibrium state is described by
$$PV=nRT\tag{8}$$
and thus
$$PdV + VdP=nRdT\tag{9}$$
$$PdV=nRdT-VdP\tag{10}$$
which we can substitute into (7) to obtain
$$dQ=C_VdT+nRdT-VdP=(C_V+nR)dT-VdP\tag{11}$$
$$\frac{dQ}{dT}=C_V+nR-V\frac{dP}{dT}\tag{12}$$
If we hold ##P## constant then
$$C_P=\left (\frac{dQ}{dT}\right )_P=C_V+nR\tag{13}$$
which tells us that the constant pressure heat capacity is larger than the constant volume heat capacity. The reason for this is that when we add heat to a gas that is allowed to expand, expansion work is done. The heat is used to increase temperature and also do expansion work.
In the case of a constant volume, no expansion work is done, so the heat capacity is smaller.
We can also write (12) as
$$\frac{dQ}{dT}=C_P-V\frac{dP}{dT}\tag{14}$$
Now, consider a quasi-static adiabatic process.
Take equations (7) and (14), but since we have an adiabatic process sub in ##dQ=0##. Thus
$$0=C_V+PdV\tag{7a}$$
$$0=C_PdT-VdP\tag{14a}$$
Thus
$$PdV=-C_V\tag{7b}$$
$$VdP=C_PdT\tag{14b}$$
and if we divide one by the other we end up with
$$\frac{dP}{P}=-\frac{C_P}{C_V}\frac{dV}{V}=-\gamma\frac{dV}{V}\tag{15}$$
where ##\gamma>1## and the exact value of ##\gamma## depends on the nature of the gas in question and is determined experimentally.
Now, for certain gases or for certain temperature ranges, it can be regarded as constant, in which case we integrate (15) to obtain
$$PV^{\gamma}=\text{constant}\tag{16}$$
This is an equation of state for all equilibrium states through which an ideal gas passes during a quasi-static adiabatic process.
My question is about what this means graphically, especially in comparison with a quasi-static isothermal process.
In the latter, we have ##P=\frac{nRT}{V}## and
$$\left (\frac{\partial P}{\partial V}\right )_T=\frac{-nRT}{V^2}=-\frac{P}{V}>-\gamma \frac{P}{V}\tag{17}$$
which simply tells us that at any point ##P, V## in a ##PV## plot, the slope at that point of the adiabatic process passing through that point is more negative than the slope at that point of the isothermal process passing through that point.
Consider the following pictorial depiction
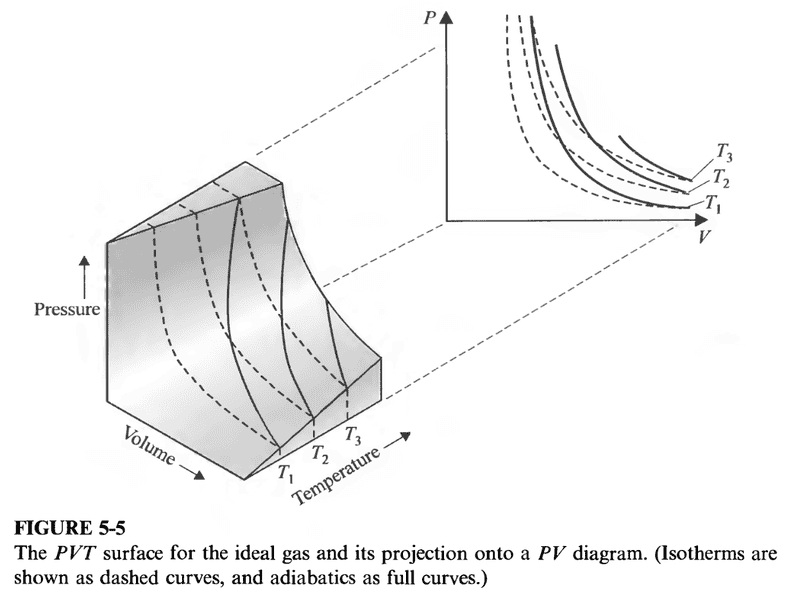
An isothermal process is represented by points on a curve that has all points at the same temperature (a dashed line above).
An adiabatic process seems to be represented by the solid lines. These are points that have varying ##P, V##, and ##T##.
Yet all we derived was equation (16). How do we know exactly what is happening to ##T##?
Is the answer simply obtained from the ideal gas equation ##PV=nRT##?
Ie, is it true that

From the first law, we have that
$$dQ = dU - dW\tag{1}$$
Now, we also have
$$dU=\left (\frac{\partial U}{\partial T} \right )_VdT + \left (\frac{\partial U}{\partial V} \right )_T dV\tag{2}$$
$$dW=-PdV\tag{3}$$
and so
$$dQ = \left (\frac{\partial U}{\partial T} \right )_VdT + \left (\frac{\partial U}{\partial V} \right )_T dV +PdV\tag{4}$$
$$=\left (\frac{\partial U}{\partial T} \right )_VdT +\left ( \left (\frac{\partial U}{\partial V} \right )_T + P \right )dV\tag{5}$$
If we consider ##V## constant, then
$$C_V=\left (\frac{dQ}{dT}\right )_V=\left (\frac{\partial U}{\partial T} \right )_V\tag{6}$$
That is, we reach an equation for the constant volume heat capacity. For some temperature change, the amount of heat equals the change in internal energy.
Therefore, from (1) we have
$$dQ=dU-dW=C_V+PdV\tag{7}$$
Since we have an ideal gas, we also know that any equilibrium state is described by
$$PV=nRT\tag{8}$$
and thus
$$PdV + VdP=nRdT\tag{9}$$
$$PdV=nRdT-VdP\tag{10}$$
which we can substitute into (7) to obtain
$$dQ=C_VdT+nRdT-VdP=(C_V+nR)dT-VdP\tag{11}$$
$$\frac{dQ}{dT}=C_V+nR-V\frac{dP}{dT}\tag{12}$$
If we hold ##P## constant then
$$C_P=\left (\frac{dQ}{dT}\right )_P=C_V+nR\tag{13}$$
which tells us that the constant pressure heat capacity is larger than the constant volume heat capacity. The reason for this is that when we add heat to a gas that is allowed to expand, expansion work is done. The heat is used to increase temperature and also do expansion work.
In the case of a constant volume, no expansion work is done, so the heat capacity is smaller.
We can also write (12) as
$$\frac{dQ}{dT}=C_P-V\frac{dP}{dT}\tag{14}$$
Now, consider a quasi-static adiabatic process.
Take equations (7) and (14), but since we have an adiabatic process sub in ##dQ=0##. Thus
$$0=C_V+PdV\tag{7a}$$
$$0=C_PdT-VdP\tag{14a}$$
Thus
$$PdV=-C_V\tag{7b}$$
$$VdP=C_PdT\tag{14b}$$
and if we divide one by the other we end up with
$$\frac{dP}{P}=-\frac{C_P}{C_V}\frac{dV}{V}=-\gamma\frac{dV}{V}\tag{15}$$
where ##\gamma>1## and the exact value of ##\gamma## depends on the nature of the gas in question and is determined experimentally.
Now, for certain gases or for certain temperature ranges, it can be regarded as constant, in which case we integrate (15) to obtain
$$PV^{\gamma}=\text{constant}\tag{16}$$
This is an equation of state for all equilibrium states through which an ideal gas passes during a quasi-static adiabatic process.
My question is about what this means graphically, especially in comparison with a quasi-static isothermal process.
In the latter, we have ##P=\frac{nRT}{V}## and
$$\left (\frac{\partial P}{\partial V}\right )_T=\frac{-nRT}{V^2}=-\frac{P}{V}>-\gamma \frac{P}{V}\tag{17}$$
which simply tells us that at any point ##P, V## in a ##PV## plot, the slope at that point of the adiabatic process passing through that point is more negative than the slope at that point of the isothermal process passing through that point.
Consider the following pictorial depiction
An isothermal process is represented by points on a curve that has all points at the same temperature (a dashed line above).
An adiabatic process seems to be represented by the solid lines. These are points that have varying ##P, V##, and ##T##.
Yet all we derived was equation (16). How do we know exactly what is happening to ##T##?
Is the answer simply obtained from the ideal gas equation ##PV=nRT##?
Ie, is it true that
Last edited: