Graphing electric potential for two positive charges

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For part (a) of this problem,

The solution is

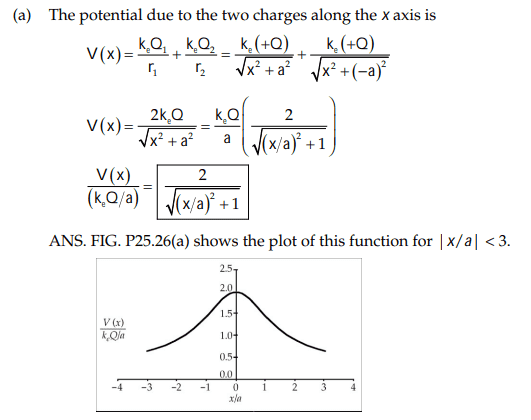
However, my solution is

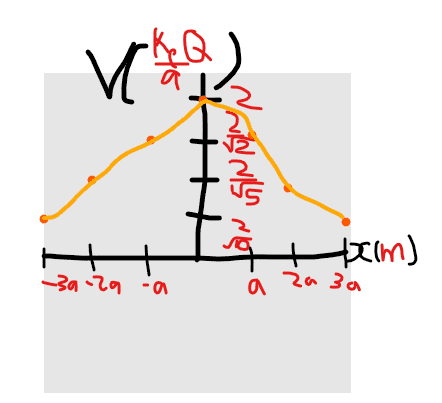
Am I correct? In the solutions that don't appear to plot the electric potential as units of $\frac {k_eQ} {a}$ like I have which the problem statement said to do.

Many thanks!

 

[kuruman]

Your plot is too crudely drawn for a direct comparison with the textbook. Not only that, but in your plot the tick marks on the vertical axis are not equally spaced as is the case in the textbook plot. So what exactly are you comparing? I suggest that you use a plotting program instead of doing it freehand. Free plotting programs exist on the internet. I went to https://www.desmos.com/calculator and created this.

 

[member 731016]

Your plot is too crudely drawn for a direct comparison with the textbook. Not only that, but in your plot the tick marks on the vertical axis are not equally spaced as is the case in the textbook plot. So what exactly are you comparing? I suggest that you use a plotting program instead of doing it freehand. Free plotting programs exist on the internet. I went to https://www.desmos.com/calculator and created this.

View attachment 321043

Yes sorry @kuruman I will graph it. I am comparing my graph which has a y-axis of $V(\frac{k_eQ}{a}) = \frac {2}{\sqrt{10}}, \frac {2}{\sqrt{5}}, \frac {2}{\sqrt{2}}, 2$ and x-axis of$x(a) = -3a, -2a, -a, a, 2a, 3a$

 

[member 731016]

Your plot is too crudely drawn for a direct comparison with the textbook. Not only that, but in your plot the tick marks on the vertical axis are not equally spaced as is the case in the textbook plot. So what exactly are you comparing? I suggest that you use a plotting program instead of doing it freehand. Free plotting programs exist on the internet. I went to https://www.desmos.com/calculator and created this.

View attachment 321043

Here is my new graph @kuruman

I am comparing the y and x axes. I am not sure whether my graph is correct or not.

Thanks!

 

[kuruman]

It is not correct. The x-axis is fine and compares directly with the textbook and my plot if $a=1$, i.e. plot $k_eQ/ a$ vs. $x/a$. The y-axis is not OK. You cannot label equally spaced intervals using unequal labels. Since there are four intervals between zero and 2 on the vertical axis, the labels should be 0.5, 1.0 and 1.5. In fact the demos plotting utility assumes that this is the case.

 

[member 731016]

It is not correct. The x-axis is fine and compares directly with the textbook and my plot if $a=1$, i.e. plot $k_eQ/ a$ vs. $x/a$. The y-axis is not OK. You cannot label equally spaced intervals using unequal labels. Since there are four intervals between zero and 2 on the vertical axis, the labels should be 0.5, 1.0 and 1.5. In fact the demos plotting utility assumes that this is the case.

Thank you for your reply @kuruman ! Whoops I see my mistake with the y-axis. Also, I've never seen the notation $x/a$ - what does it mean please?

I will post a new graph soon.

 

[member 731016]

It is not correct. The x-axis is fine and compares directly with the textbook and my plot if $a=1$, i.e. plot $k_eQ/ a$ vs. $x/a$. The y-axis is not OK. You cannot label equally spaced intervals using unequal labels. Since there are four intervals between zero and 2 on the vertical axis, the labels should be 0.5, 1.0 and 1.5. In fact the demos plotting utility assumes that this is the case.

Here's the new graph @kuruman ,

 

[kuruman]

That's fine except for the old labels on the vertical axis that need to be removed. Just so that you know. You don't have to do it because it's not going to be graded.

 

[member 731016]

That's fine except for the old labels on the vertical axis that need to be removed. Just so that you know. You don't have to do it because it's not going to be graded.

Thank you @kuruman , but I still don't see how my and their graphs are equivalent. On their graph the y-axis is $\frac {V(x)a} {k_eQ}$ and my graph it is $V (\frac {k_eQ} {a})$

For the x-axis, their graph is $x/a$ and my graph is $x$.

Correct me if I am wrong, but the notation $x$ is the same as $x(a)$. I'm not sure why.

Many thanks!

 

[member 731016]

Thank you @kuruman , but I still don't see how my and their graphs are equivalent. On their graph the y-axis is $\frac {V(x)a} {k_eQ}$ and my graph it is $V (\frac {k_eQ} {a})$

For the x-axis, their graph is $x/a$ and my graph is $x$.

Correct me if I am wrong, but the notation $x$ is the same as $x(a)$. I'm not sure why.

Many thanks!

EDIT: Sorry I meant that the notation $x$ is not the same as $x(a)$

 

[robphy]

This may help https://www.desmos.com/calculator/zu8hbssbxp . (Visit to see how the pieces below are created.)

Vary the a-slider.

(By the way, you can copy-paste equations from desmos (as TeX, acceptable for MathJax)... just surround by itex and /itex in square brackets .)

V_{factor}=\frac{2}{\sqrt{\left(x_{factor}\right)^{2}+1}} (right-click the equation)
where
V=\frac{kQ}{a}\left(\frac{2}{\sqrt{\left(\frac{x}{a}\right)^{2}+1}}\right)

V_{fac}=\frac{V}{\left(\frac{kQ}{a}\right)} and x_{fac}=\frac{x}{a} (different variable names given in Desmos) are both dimensionless quantities.
(\frac{kQ}{a} carries the units of Volts, and \frac{x}{a} carries the units of meters.)Note that if the [implied] right-hand-side of an entry has a free variable, it becomes the independent variable.

 

[member 731016]

This may help https://www.desmos.com/calculator/zu8hbssbxp . (Visit to see how the pieces below are created.)

Vary the a-slider.

(By the way, you can copy-paste equations from desmos (as TeX, acceptable for MathJax)... just surround by itex and /itex in square brackets .)

V_{factor}=\frac{2}{\sqrt{\left(x_{factor}\right)^{2}+1}} (right-click the equation)
where
V=\frac{kQ}{a}\left(\frac{2}{\sqrt{\left(\frac{x}{a}\right)^{2}+1}}\right)

V_{fac}=\frac{V}{\left(\frac{kQ}{a}\right)} and x_{fac}=\frac{x}{a} (different variable names given in Desmos) are both dimensionless quantities.
(\frac{kQ}{a} carries the units of Volts, and \frac{x}{a} carries the units of meters.)Note that if the [implied] right-hand-side of an entry has a free variable, it becomes the independent variable.

View attachment 321094

Thank you for your reply @robphy ! I kind of get what you are saying that my and their graphs are equivalent, is that correct?

Many thanks!

 

[robphy]

Type in your equation in that Desmos file and see if it matches.

 

[member 731016]

Type in your equation in that Desmos file and see if it matches.

Thank you for your reply @robphy! How do I do that sorry?

Many thanks!

 

[robphy]

On that Desmos file, add a blank entry or scroll down to find one blank entry.
Type in your formula, using variable names not already used.

 

[member 731016]

On that Desmos file, add a blank entry or scroll down to find one blank entry.
Type in your formula, using variable names not already used.

Thank you @robphy! I will give it a try and post it.

 

[member 731016]

On that Desmos file, add a blank entry or scroll down to find one blank entry.
Type in your formula, using variable names not already used.

Thanks @robphy - it seems to be working! However why dose it work?

Many thanks!