Graphs of Frequency for Car Moving in a Circle

[Knightycloud]

Homework Statement

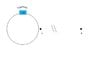
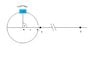
A car with a horn making a frequency of 'f' Hz is driven in a circle with a radius of 'r' m. The uniform velocity of the car is v ms^-1.
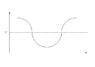
Draw graphs showing the frequency observes by the observer who is standing on;
a) Position A
b) Position B

(Position B is very far from the circle)

Homework Equations

f' = f($\frac{u}{u\pm v}$)

u - Velocity of sound
v - Velocity of the car

The Attempt at a Solution

*Please refer the attachments*
My answer for this one is only the position A is having a variation in the frequency while the position B observes the same frequency of 'f' Hz

Am I Right or please help me with this one! :)

 

[haruspex]

When at position B, is the car a constant distance from the observer? If not, it must be sometimes moving towards the observer and sometimes away.
I suggest you should show the position of the car on the horizontal axis of the graphs, e.g. in terms of theta, where the car's position is at (r, theta) in polar coordinates centred on the centre of the circle. The comparison between the two graphs is interesting.

 

[Knightycloud]

Nope, both positions A & B are at constant distances and they're not moving either. So you mean both positions observe a variation in the frequency regardless how far they're from the source?
And is that graph I drew correct?

 

[haruspex]

Nope, both positions A & B are at constant distances and they're not moving either.

No, you misunderstand my question. When the observer is at position B, is the car at constant distance from the observer?

So you mean both positions observe a variation in the frequency regardless how far they're from the source?

Yes.

And is that graph I drew correct?

Yes, but you need to mark the x-axis to show which point on the graph corresponds to which position of the car.

 

[Knightycloud]

No, you misunderstand my question. When the observer is at position B, is the car at constant distance from the observer?

No the car keeps moving and the observer is still.

Am I correct if I say, both positions plot the same graph with same values? I mean in the doppler equation, only variables are the velocities and the frequency. There's no mention about how far the observer is from the object.

 

[haruspex]

Am I correct if I say, both positions plot the same graph with same values? I mean in the doppler equation, only variables are the velocities and the frequency. There's no mention about how far the observer is from the object.

No, the graphs are similar but not the same. For one thing, the peaks and troughs don't line up, which is why I believe you must show the x-coordinates for a proper comparison.
If I were doing this problem I would develop the actual equations, but from the way the question is worded I feel they don't expect you to do that. Instead, you need to sketch the graphs from simple reasoning.
Denote the position of the car by theta as I described in an earlier post. So when the car is near A theta = 0, and when it's furthest from A theta = pi. With the observer at A, for what theta(s) is the observed frequency:
- highest?
- lowest?
- same as emitted frequency?
- changing most rapidly?
Same questions at B.

 

[Knightycloud]

I've changed the graph accordingly. Is it correct now? :)

 

[haruspex]

B is about right, but A is significantly off. At what theta will the car be traveling straight towards A?
Here's a question I missed before: The peak observed frequency will be when the car is moving straight towards the observer, right? Does the distance affect this?

 

[Knightycloud]

So that means if I draw a tangent to the circle from the point B, that is the moment when the car is moving straight to the point and that's when the highest frequency is observed?

 

[Knightycloud]

And another thing, Are these both positions observe the same highest frequency? Or is it differs?

 

[haruspex]

So that means if I draw a tangent to the circle from the point B, that is the moment when the car is moving straight to the point and that's when the highest frequency is observed?

Yes, and the lowest if moving away.

Are these both positions observe the same highest frequency? Or is it differs?

You quoted the formula in the OP. Does distance figure in it?

 

[Knightycloud]

Ok then, From what I understood, the highest frequency observed is the same for both positions and the only difference is 'the time (In this case; θ)' when they observe it. Right? If I'm correct here this one's settled! :D

 

[haruspex]

Ok then, From what I understood, the highest frequency observed is the same for both positions and the only difference is 'the time (In this case; θ)' when they observe it. Right? If I'm correct here this one's settled! :D

The shape is also rather different. In particular, for what thetas are the highest and lowest frequencies heard at A?

 

[Knightycloud]

Yea the shapes are different! But the peaks and bottoms are at the same values, right?

 

[haruspex]

Yea the shapes are different! But the peaks and bottoms are at the same values, right?

The same heights, yes, not the same theta values. What is the most striking difference?

 

[Knightycloud]

Difference is the start point and the end point of a cycle.

 

[haruspex]

Difference is the start point and the end point of a cycle.

Too vague. Please either post a picture or try to be a lot more descriptive.

 

[Knightycloud]

Is this one the correct graph?

 

[haruspex]

No, the shape is significantly different in the A case. Pls try to answer this question I keep asking you: at approx what values of theta will the frequency be highest and lowest at A? Remember, since the speed is constant, this depends entirely on the extent to which the motion is towards or away from A.

 

[Knightycloud]

Draw two tangents to the circle from point A. One tangent represents the car coming in and the other one represents the car going out. That is when the highest and the lowest are observed. Theta values are -θ and +θ where theta is measured taking AO as the base.

Am I close enough?

 

[Knightycloud]

I drew the graph accordingly.

 

[haruspex]

Much better. My only quibble now is that the slope is too steep around θ = pi. It will be quite gradual there. The curve should be a bit more like a sawtooth.

 

[Knightycloud]

OK! So if I get that one corrected it's over? Thanks a lot! You made me understand it other than giving a simple 'answer'.

 

[haruspex]

Just to finish this off... if you take A as being on the circle then with a little geometry you can see that the speed away from the observer will vary as cos(θ/2) as θ runs from 0 to 2pi. Plot that and compare with your sketch.

 

[Knightycloud]

Yea I'll try that too. Thanks again! :)