- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is the Colatitude Angle in Gravitation?
- Thread starter cupid.callin
- Start date
-
- Tags
- Angle Gravitation
In summary, the "gravitation - colatitude angle" is an angle between the direction of gravity and the surface normal of a body. It is calculated using trigonometry and can be affected by factors such as the body's size and shape, rotation rate, and location on its surface. This angle is important in the study of gravitation as it helps to understand the distribution and strength of gravity on a body's surface and has practical applications in fields such as geodesy and satellite orbit calculations.
Physics news on Phys.org
- #2
gneill
Mentor
- 20,989
- 2,934
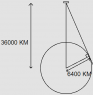
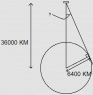
Geostationary satellites have a specific orbital radius, and orbit in a particular plane. The Earth is spherical. As you travel northwards (or southwards), at what colatitude will the satellite drop below the viewing horizon?
- #3
- #4
gneill
Mentor
- 20,989
- 2,934
Colatitude: http://en.wikipedia.org/wiki/Colatitude
- #5
- #6
gneill
Mentor
- 20,989
- 2,934
FAQ: What is the Colatitude Angle in Gravitation?
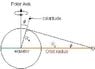
What is the "gravitation - colatitude angle"?
The "gravitation - colatitude angle" is the angle between the direction of gravity and the surface normal of a body. It is typically measured from the body's rotational axis and can help determine the strength and direction of the gravitational force on an object.
How is the "gravitation - colatitude angle" calculated?
The "gravitation - colatitude angle" can be calculated using trigonometry, specifically the cosine function. The formula is cos(θ) = z/r, where θ is the angle, z is the distance from the body's rotational axis to the point of interest, and r is the distance from the center of the body to the point of interest.
What factors can affect the "gravitation - colatitude angle"?
The "gravitation - colatitude angle" can be affected by several factors including the size and shape of the body, its rotation rate, and the position of the point of interest. It can also vary depending on the location on the body's surface.
Why is the "gravitation - colatitude angle" important in the study of gravitation?
The "gravitation - colatitude angle" is important because it helps to understand the distribution and strength of gravity on a body's surface. It is also used in the study of celestial bodies, such as planets and moons, to determine their gravitational fields and how they affect objects in their vicinity.
How is the "gravitation - colatitude angle" used in practical applications?
The "gravitation - colatitude angle" has practical applications in fields such as geodesy, where it is used to measure the Earth's gravitational field and determine its shape and size. It is also used in satellite orbit calculations, as the angle affects the trajectory and stability of satellites in orbit around a body.
Similar threads
- Replies
- 4
- Views
- 490
- Replies
- 4
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 3
- Views
- 5K
- Replies
- 18
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 5
- Views
- 3K
- Replies
- 8
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 28
- Views
- 2K
Share: