ognik
- 626
- 2
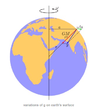
Q: "The dependence of fee fall acceleration g on geographical latitude $\phi$ at sea level is given by $g=g_0\left(1+0.0053 Sin^2\phi\right)$. What is the southward displacement near $\phi = 30 ^{\circ}$ that changes g by 1 part in $10^8$?"
This is in a section on gradient ($\nabla$) but I can't visualise the directions involved. I assume the equator is $\phi = 0^{\circ}$ so is the gradient of g pointing at the centre of the Earth at the equator? and $f\left(\phi\right)$ is along the surface of the earth? Then is $\phi = 30 ^{\circ}$ pointing parallel to the gradient at the centre?
Maybe I should be using $df(\phi) = C_1 - C_2 = \Delta C = \left(\nabla f(\phi) \right).dr$ with $df(\phi)$ the '1 part in $10^8$' and dr is the southward displacement?
This is in a section on gradient ($\nabla$) but I can't visualise the directions involved. I assume the equator is $\phi = 0^{\circ}$ so is the gradient of g pointing at the centre of the Earth at the equator? and $f\left(\phi\right)$ is along the surface of the earth? Then is $\phi = 30 ^{\circ}$ pointing parallel to the gradient at the centre?
Maybe I should be using $df(\phi) = C_1 - C_2 = \Delta C = \left(\nabla f(\phi) \right).dr$ with $df(\phi)$ the '1 part in $10^8$' and dr is the southward displacement?