- #1
Artlav
- 162
- 1
Gravity of a massive body slows time rate, the closer the clock to it, the slower it goes, according to general relativity.
What i didn't quite understood is what is responsible for the dilation?
That is, is it dependable on the gravity acceleration, curvature of space, or something else?
There was an experiment with one atomic clock being raised to about 10Km and the other staying back on Earth, with the up going one then showing the difference.
Now, if we put one clock at the center of the Earth, and one on the surface, what will be the result?
What i mean:
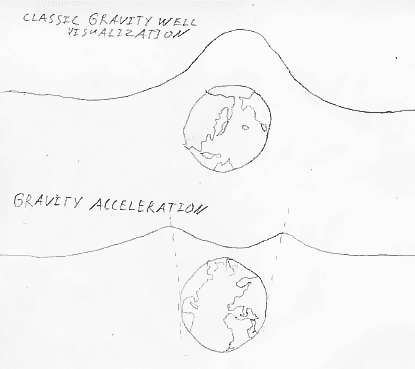
There is no gravity acceleration in the center of the Earth due to it's own mass and "the space is flat" for what i can comprehend, so will the time rate be the same as in relatively flat outer space near Earth, faster than on the surface, same, slower, or entirely different?
If it will be slower than on the surface, then what is physically different in the center of the Earth (harsh pressure/temperature conditions aside) that causes the dilation?
.
What i didn't quite understood is what is responsible for the dilation?
That is, is it dependable on the gravity acceleration, curvature of space, or something else?
There was an experiment with one atomic clock being raised to about 10Km and the other staying back on Earth, with the up going one then showing the difference.
Now, if we put one clock at the center of the Earth, and one on the surface, what will be the result?
What i mean:
There is no gravity acceleration in the center of the Earth due to it's own mass and "the space is flat" for what i can comprehend, so will the time rate be the same as in relatively flat outer space near Earth, faster than on the surface, same, slower, or entirely different?
If it will be slower than on the surface, then what is physically different in the center of the Earth (harsh pressure/temperature conditions aside) that causes the dilation?
.