-gre.ge.11 x,y of fourth corner of diagonal

[karush]

In the standard (x,y) coordinate plane below, 3 of the vertices of a rectangle are shown. Which of the following is the 4th vertex of the rectangle?

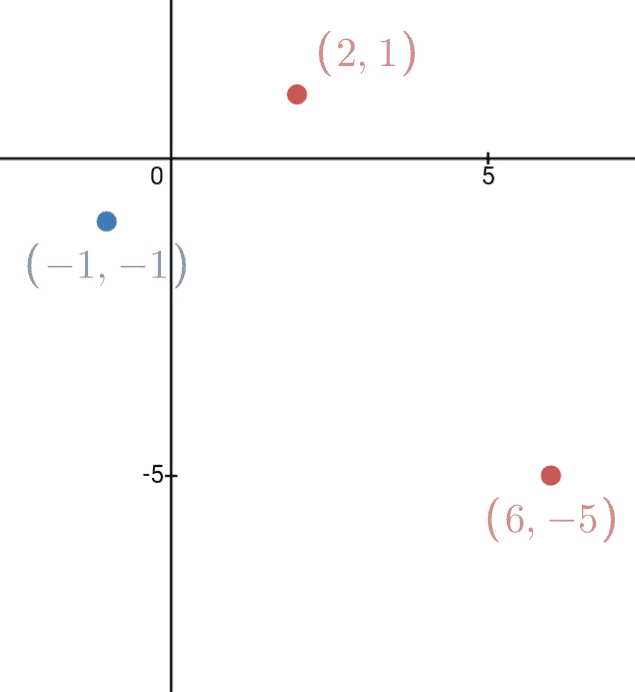
sorry about the huge image but couldn't find where to scale it down
a. (3,-7)
b. (4,-8)
c. (5,-1)
d. (8,-3)
e. (9,-3)

ok I don't think we need a bunch of equations to do this
$\delta$ x of the with is 3
$\delta$ y of the width is 2

so the fourth corner is
(6-3,-5-2)=(3,-7)

 

[HOI]

I get that from (2, 1) to (6, -5) is a "delta" of (6- 2, -5- 1)= (4, -6). So the line parallel to that through (-1, -1) goes through (-1+ 4, -1- 6)= (3, -7) also.

 

[topsquark]

Just to cover all bases I'd first show that the lines (-1, -1) to (6, -5) and (2, 1) to (-1, -1) are not perpendicular so the line from (-1, -1) to (6, -5) must be a diagonal.

-Dan

 

[karush]

good point
by observation it sure looks like a rectangle