Ground state energy of cube-like potential wells

[hilbert2]

TL;DR Summary

An estimate for 3d potential wells of different depths and shapes is calculated with quantum diffusion monte carlo.

In some other thread someone mentioned that a 3D cubic potential well always has a ground state that is a bound state, but a spherical well doesn't necessarily have if it's too shallow.

I calculated some results for 3d cubes, spheres and surfaces of form $x^{2n}+y^{2n}+z^{2n}=r^{2n}$, which look like

4th order (n=2):

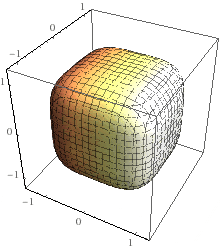
6th order (n=3):

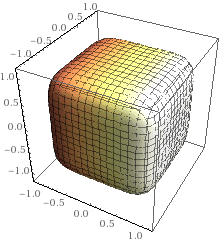
10th order (n=5):

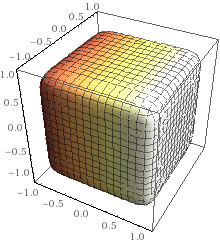
and are the more cube-like the larger the exponent $2n$ is. The ground state energy was obtained with an old diffusion monte carlo code from

https://github.com/m0baxter/DMC

with the potential energy $V(x,y,z)$ set to some constant value $V$ outside the well and to $0$ inside it. I'll post the graphs of the results here in case someone finds them interesting.

For well depth $V=1500$, similar to a hard-walled box, the results for spheres, cubes and things between them were like in this image:

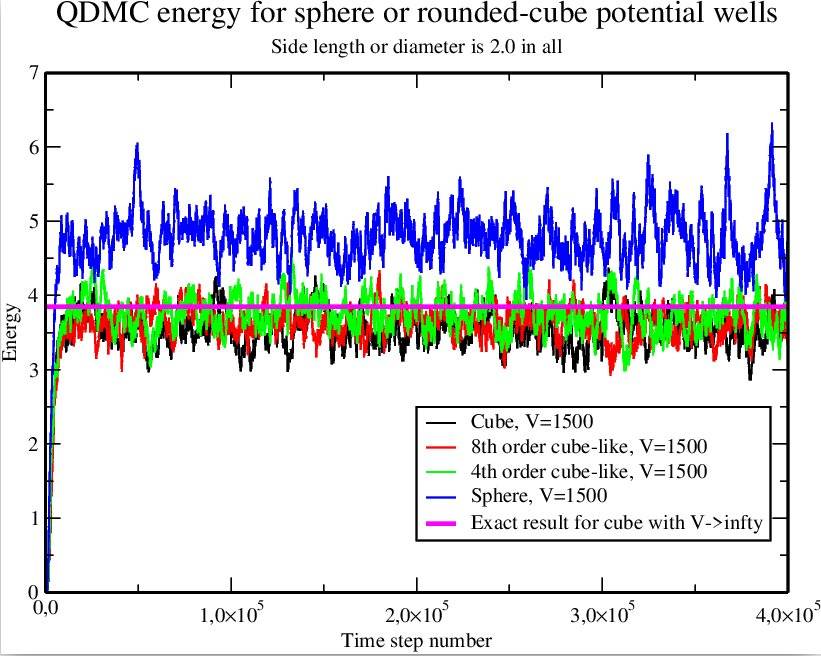The energy converges to much the same value with a cubic box and the $x^n + y^n + z^n = r^n$ as long as the $n>4$. With $n=4$ there's a small but clear difference to the cube if you calculate the average of the energy values after convergence ($t>10^5$). The ground state for these was near the exact result, $E=3.85$, of a box with that side length and hard walls ($V\rightarrow\infty$). I think the energies are a bit less than that because $V$ is only large but finite.

If the graph for the spherical well is compared to the exact result for a sphere with hard walls, then it looks like this:

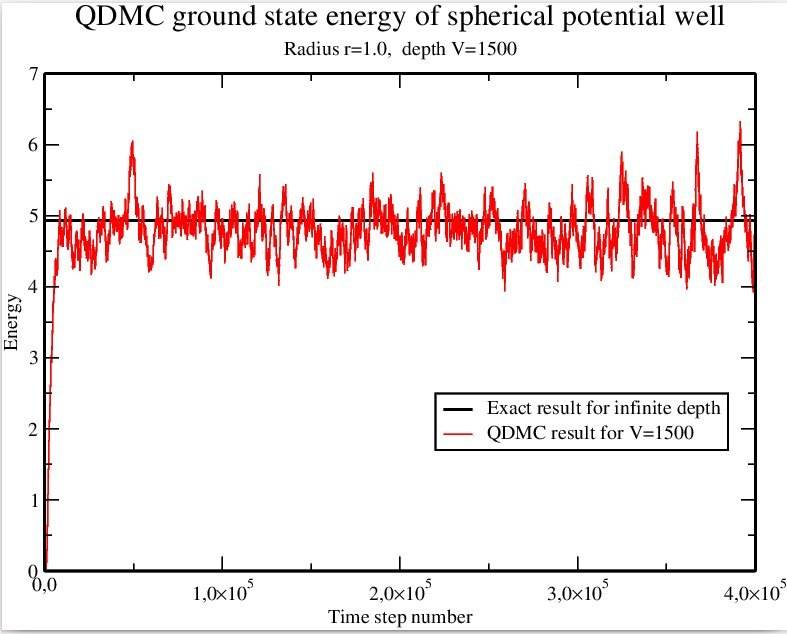
So there's a good agreement there as well.

The same result calculated for potential wells of same radius and a potential step of only $V=1$ looks like

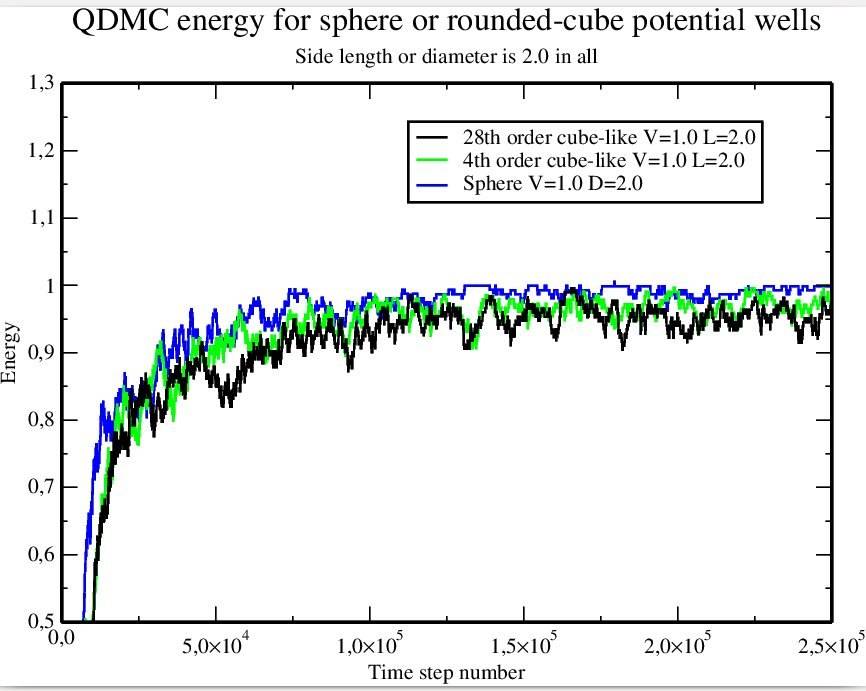
So there's a less clear difference between a cube and a sphere potential well when the potential well is shallow. The 28th order surface can for any computational physicist's interests be seen as exactly the same as a cube.

The QDMC calculation takes a lot more time for less deep potential wells. Actually, it doesn't seem to be convenient to try to test whether the ground state looks like a bound state for a really low well depth like $V=10^{-3}$. This was the result I was interested in. Maybe I could calculate ground state energies for different well depths and extrapolate to zero depth to see what happens. To do that, it's probably necessary to include surfaces like $|x|^q + |y|^q +|z|^q = r^q$ with $q$ a rational number between $2$ and $4$ because for integer values only there are not enough data points. The similarity of the results in the first image makes me somehow expect that almost all properties of $x^n + y^n + z^n = r^n$ potential wells, including the existence of a bound state, are the same as for a cube when $n>4$.

So, this was an Insight-like example of a ground state energy calculation with QDMC. In some book containing a physics lecture by E. Fermi there actually was a cube-rounded-from-corners potential well used in an atomic nucleus model, but I couldn't find any other examples of applications.

CORRECTION: The ground state energy of an infinite cube-shaped well with side length 2.0 should be $E_0 = \frac{3\pi^2}{8} \approx 3.7$, not the 3.85 in the first picture. That's why the DMC graphs seemed to converge to a smaller value than they should. The particle mass in all simulations was $m=1$, and the Planck constant was also $\hbar =1$ as in atomic-like units.

 

[hilbert2]

It seems that the exponent of the surface $|x|^q +| y|^q + |z|^q = r^q$ needs to be as low as $q=2.5$ for the ground state energy to be about halfway between that of a sphere and a cube.

If someone else wants to do the simulation, the "dmc.cpp" source code file from that GitHub page needs to be edited to have this kind of "main" and "V" functions to be the same as what I did.

double V( std::array<double, 3> &x ) {
if(pow(x[0],4)+pow(x[1],4)+pow(x[2],2.5)<1.0) return 0.0;
else return 1500.0;
}

int main() {

   const int d = 3;                  //Spatial dimension
   const int s = 1;                  //Number of particles
   const int dp = d*s;               //Effective dimension.
   int N0 = 1000;                     //Intial numberof points.
   const int maxN = 10000;            //Maximum number of points.
   int nb = 200;                     //Number of bins for wave function histogram.
   double xmin = -10;                 //Lower bound of grid
   double xmax = 10;                  //Upper bound of grid
   double timeStep = 0.0001;           //Time step.
   double relaxTime = 20;            //Time to wait for convergence.
   double alpha = 5.0;               //Update parameter for energy.

   std::array<double, 3> x0 = { 0.0, 0.0, 0.0 };  //Initial position of particles.
   std::function<double (std::array<double, dp> &)> potential = V; //The Potential.

   runSimulation<maxN, dp>( s, N0, nb, xmin, xmax, timeStep, relaxTime, alpha, x0, potential, true, true );

   return 0;
}

 

[Haborix]

You've been playing with a couple of fun problems lately. Is this quarantine induced?

 

[hilbert2]

You've been playing with a couple of fun problems lately. Is this quarantine induced?

Possibly. Also, to keep these tools in memory just in case I can some day afford to get a PhD degree in the future.

Some other things I could calculate with this are the first and second order coefficients for a perturbation series $E_0 = C_0 + C_1 \lambda + C_2 \lambda^2 + \dots$ with $\lambda$ as in

$|x|^{2+\lambda} + |y|^{2+\lambda} + |z|^{2+\lambda} = r^{2+\lambda}$,

and the same for a perturbation that stretches the potential well in one direction to make it ellipsoid or parallelepiped-like.

I also have to look for a way to quantify how closely a function $\psi (x,y,z)$ can be approximated with a product $\psi (x,y,z) = X(x)Y(y)Z(z)$ or $\psi (r,\theta ,\phi ) = R(r)\Theta (\theta) \Phi (\phi)$. The most obvious one would be to compare the energy expectation value of the exact ground state wavefunction and its Hartree approximation.

Edit: Defining the parameter $q$ as in $|x|^{2+q} + |y|^{2+q} + |z|^{2+q} = r^{2+q}$, meaning that $q=0$ corresponds to a spherical potential well, the results for ground state energy as a function of $q$ for potential step of $1500$ and well diameter $2.0$ are as in the images:

The parameters in the second order curve fit $E_0 \approx C_0 + C_1 q + C_2 q^2$ were

$C_0 = 4.791$
$C_1 = -1.974$
$C_2 = 1.662$

The energy at the limit of small or large $q$ are a bit (3% to 5%) lower than the values for $V\rightarrow\infty$, probably because the $V$ had a finite value $1500$ in the calculations.