musicgold
- 303
- 19
- Homework Statement
- Not a homework problem. I wanted to find out what is the best guess for the number of throws required to get a 6 on a dice.
- Relevant Equations
- So I ran a simulation and the results seem counterintutive. See the results below.
The table below shows the probabilities for getting a 6 in up to 20 throws.
1. I know that the expected number of throws is 6, but that number doesn't seem to be a useful guide here, even in the long run. 1 throw seems to be the best guess. What am I missing?
2. The cumulative probability of getting a 6, crosses the 50% mark at around 4. How do we reconcile that fact with the expected number of throws of 6?
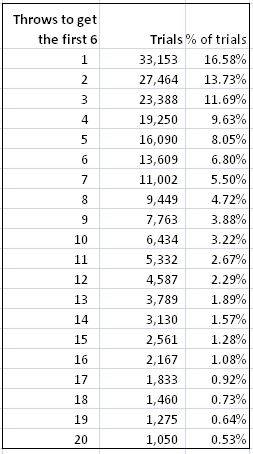
Thanks
1. I know that the expected number of throws is 6, but that number doesn't seem to be a useful guide here, even in the long run. 1 throw seems to be the best guess. What am I missing?
2. The cumulative probability of getting a 6, crosses the 50% mark at around 4. How do we reconcile that fact with the expected number of throws of 6?
Thanks