eyeweyew
- 35
- 6
- Homework Statement
- Results from simple nodal analysis for non-inverting amplifier are not the same as results after converting the feedback portion to h-parameters circuit
- Relevant Equations
- Nodal analysis and h-parameter model
For a standard non-inverting amplifier as below:
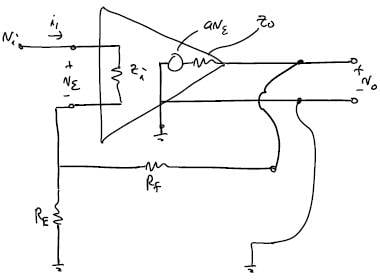
With nodal analysis, I got $$\frac {v_o} {v_i}=\frac {R_EZ_o+aZ_iR_E+aZ_iR_f} {R_ER_f + R_EZ_i + R_EZ_o + R_fZ_i + Z_iZ_o + R_EaZ_i}$$
However, with the feedback network of the amplifier converted to a h-parameter network as below:
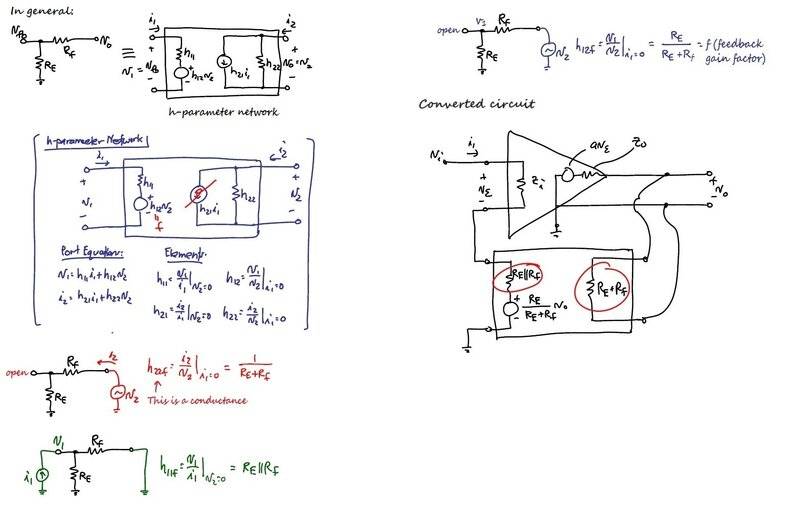
With nodal analysis on this converted circuit, I got $$\frac {v_o} {v_i}=\frac {aZ_i(R_E + R_f)^2} {R_ER_f^2 + R_E^2R_f + R_E^2Z_i + R_f^2Z_i + 2R_ER_fZ_i + R_ER_fZ_o + R_EZ_iZ_o + R_fZ_iZ_o + R_E^2aZ_i + R_ER_faZ_i}$$
I checked with Matlab to make sure the two results are different. My question is, are they suppose to produce different results? If so, why are they different? My prof is showing this so I expected they should be equivalent and produce same results.
With nodal analysis, I got $$\frac {v_o} {v_i}=\frac {R_EZ_o+aZ_iR_E+aZ_iR_f} {R_ER_f + R_EZ_i + R_EZ_o + R_fZ_i + Z_iZ_o + R_EaZ_i}$$
However, with the feedback network of the amplifier converted to a h-parameter network as below:
With nodal analysis on this converted circuit, I got $$\frac {v_o} {v_i}=\frac {aZ_i(R_E + R_f)^2} {R_ER_f^2 + R_E^2R_f + R_E^2Z_i + R_f^2Z_i + 2R_ER_fZ_i + R_ER_fZ_o + R_EZ_iZ_o + R_fZ_iZ_o + R_E^2aZ_i + R_ER_faZ_i}$$
I checked with Matlab to make sure the two results are different. My question is, are they suppose to produce different results? If so, why are they different? My prof is showing this so I expected they should be equivalent and produce same results.