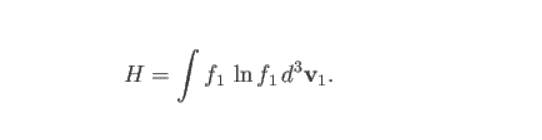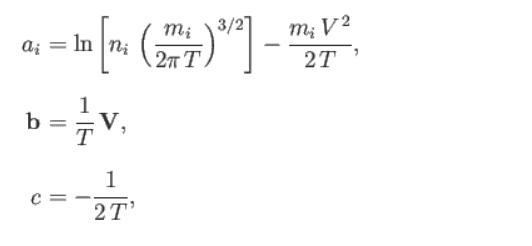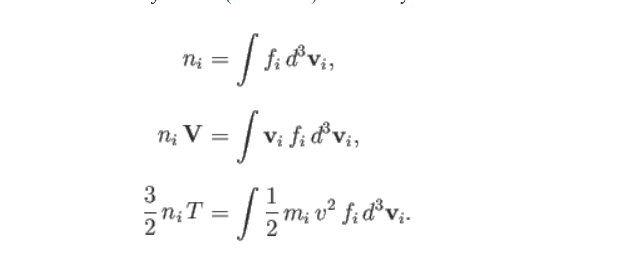H-Theorem and Lagrange multipliers

[VVS2000]

so I was studying H theorem from Richard Fitzpartic's site.
https://farside.ph.utexas.edu/teaching/plasma/Plasma/node35.html
Given H,

they consider the following equation

and set the constants as

I want to understand how they got these particular values for a, b &c
can we consider the following as constraints and a b c as lagrange multipliers and solve for them?

or if there are any other ways to obtain a b c plz do tell
thanks in advance

 

[vanhees71]

It's obviously for an ideal gas, for which we know the phase-space-distribution function exactly (let's take a monatomic gas for simplicity):
$$f=\frac{1}{(2 \pi \hbar)^3} \exp[-(\vec{p}^2-\mu)/(2m kT)].$$
Now comes the subtle point! To define the entropy (or the neg-entropy) you need to define it relative to "full information", and you have to make the argument of the ln dimensionless. What is "full information"? According to quantum theory it's that the phase-space volume the particle is contained in is determined by the uncertainty relation of position and momentum, i.e., in a volume of $(2 \pi \hbar)^3$. So the entropy is
$$S=-H=-V \int \mathrm{d}^3 p f(p) [\ln[f/(2 \pi \hbar)^3]-1]-V k \int_{\mathbb{R}^3} \frac{1}{(2 \pi \hbar)^3} \exp[-(\vec{p}^2-\mu)/(2m kT)] \frac{\vec{p}^2-\mu}{2m k T}=n V \left (\frac{3 k}{2}-\frac{\mu}{T} \right)$$
with
$$n=\frac{N}{V}=\int_{\mathbb{R}^3} \mathrm{d}^3 p f(\vec{p})=(\frac{V (k m T)^{3/2}}{2 \sqrt{2 \pi^3} \hbar^3} \exp[\mu/(k T)].$$
Using this to eliminate $\mu/T$ in the formula for $S$, leads to
$$S=n V \left [\frac{5 k}{2} - k \ln \left (\frac{2 \sqrt{2 \pi^3 n} \hbar^3}{(m k T)^{3/2}} \right ) \right],$$
which is the Sackur-Tetrode formula,
https://en.wikipedia.org/wiki/Sackur–Tetrode_equation

as can be derived by using $U=3 N k T/2=3 n V kT/2$.

 

[VVS2000]

It's obviously for an ideal gas, for which we know the phase-space-distribution function exactly (let's take a monatomic gas for simplicity):
$$f=\frac{1}{(2 \pi \hbar)^3} \exp[-(\vec{p}^2-\mu)/(2m kT)].$$
Now comes the subtle point! To define the entropy (or the neg-entropy) you need to define it relative to "full information", and you have to make the argument of the ln dimensionless. What is "full information"? According to quantum theory it's that the phase-space volume the particle is contained in is determined by the uncertainty relation of position and momentum, i.e., in a volume of $(2 \pi \hbar)^3$. So the entropy is
$$S=-H=-V \int \mathrm{d}^3 p f(p) [\ln[f/(2 \pi \hbar)^3]-1]-V k \int_{\mathbb{R}^3} \frac{1}{(2 \pi \hbar)^3} \exp[-(\vec{p}^2-\mu)/(2m kT)] \frac{\vec{p}^2-\mu}{2m k T}=n V \left (\frac{3 k}{2}-\frac{\mu}{T} \right)$$
with
$$n=\frac{N}{V}=\int_{\mathbb{R}^3} \mathrm{d}^3 p f(\vec{p})=(\frac{V (k m T)^{3/2}}{2 \sqrt{2 \pi^3} \hbar^3} \exp[\mu/(k T)].$$
Using this to eliminate $\mu/T$ in the formula for $S$, leads to
$$S=n V \left [\frac{5 k}{2} - k \ln \left (\frac{2 \sqrt{2 \pi^3 n} \hbar^3}{(m k T)^{3/2}} \right ) \right],$$
which is the Sackur-Tetrode formula,
https://en.wikipedia.org/wiki/Sackur–Tetrode_equation

as can be derived by using $U=3 N k T/2=3 n V kT/2$.

OK I get what you're trying to say but I am not seeing how this is related to my question

 

[vanhees71]

After correcting the formula for $H=-S$ you get what I wrote. Now you can Galilei-boost this to an arbitrary inertial frame, where the gas moves with a velocity $\vec{V}$ to get the coefficients you look for.

 

[VVS2000]

After correcting the formula for $H=-S$ you get what I wrote. Now you can Galilei-boost this to an arbitrary inertial frame, where the gas moves with a velocity $\vec{V}$ to get the coefficients you look for.

I am so sorry again, when you mean Galilei boost, where exactly am I supposed to apply galilean transformation? I am really sorry If I come accross as a bit naive
I am just not able to see it

 

[vanhees71]

The Galilei boost for $V$ obviously is $V'=V$ and $\vec{p}'=\vec{p}-m\vec{v}$. From this you get
$$f(\vec{p})=f(\vec{p}'+m \vec{v}).$$
Use this in the formula for $S$. You don't need to calculate more integrals, because they are all calculated for $\vec{v}=0$.

 

[vanhees71]

After some PM discussion, I think, I misunderstood the question. Of course, it's also clear that $S$ is a Galilei invariant. So here's my answer to what I believe is the original question:
Obviously I misunderstood your question. Your idea in #1 is correct. The distribution function derived from the H-theorem is that of local thermal equilibrium. It's the distribution function for an ideal gas with center-of-mass velocity $\vec{v}$, which you get from the standard Boltzmann distribution by a Galilei boost. For the gas at rest it's

$$f'(\vec{p}')=\frac{1}{(2 \pi \hbar)^3} \exp \left [-\frac{1}{kT} \left (\frac{\vec{p}^{\prime 2}}{2m}-\mu \right )\right].$$

In the frame, where the gas moves with velocity $\vec{v}$ you have

$$\vec{p}=\vec{p}'+m \vec{v}.$$

The distribution function is a scalar under Galilei boosts, i.e., you have

$$f(\vec{p})=f'(\vec{p}')=f'(\vec{p}-m \vec{v})= \frac{1}{(2 \pi \hbar)^3} \exp \left [-\frac{1}{kT} \left (\frac{(\vec{p}-m\vec{v})^2}{2m}-\mu \right )\right].$$

It's easy to calculate the expectation values for the total particle number, the total momentum, and the total energy in this frame, and this gives you indeed the Lagrange parameters $a_i$, $\vec{b}$, and $c$.
For the latter, note that temperature is related to the total energy in the (local) rest frame of the medium, i.e., to

$$E'=V \int_{\mathbb{R}^3} \mathrm{d^3 p} \frac{\vec{p}^{\prime 2}}{2m} f'(\vec{p}')=\frac{3}{2} N k T,$$

where the particle number is given by

$$N=V \int_{\mathbb{R}^3} \mathrm{d^3 p'} f'(\vec{p}')=V \int_{\mathbb{R}^3} \mathrm{d^3 p} f(\vec{p}) = \left (\frac{mkT}{2} \right)^{3/2} \frac{V}{\hbar^3} \exp \left (\frac{\mu}{kT} \right)=nV.$$

For the total momentum you get

$$\vec{P}=V \int_{\mathbb{R}^3} \mathrm{d}^3 p \vec{p} f(\vec{p}) = V \int_{\mathbb{R}^3} \mathrm{d}^3 p' (\vec{p}'+m \vec{v}) f'(\vec{p}') = N m \vec{v},$$

where I've used that in the rest frame the total momentum vanishes.

 

[TSny]

so I was studying H theorem from Richard Fitzpartic's site.
https://farside.ph.utexas.edu/teaching/plasma/Plasma/node35.html

I want to understand how they got these particular values for a, b &c

The distribution function $f_i$ is assumed to be of the form $$\ln f_i = a_i + m_i \mathbf{b}\cdot \mathbf{v}_i + m_i c v_i^2$$ where $a_i, \mathbf{b},$ and $c$ are constants.

Then the constants $n_i, \mathbf{V},$ and $T$ are defined in the link in terms of the constants $a_i, \mathbf{b},$ and $c$ by the equations
$$\begin{align*}
a_i & = \ln\left[n_i \left(\frac{m_i}{2 \pi T}\right)^{3/2}\right] - \frac{m_i V^2}{2T} \\
b & = \frac{1}{T}\mathbf{V}\\
c & = -\frac{1}{2T}
\end{align*}$$ At this point, the physical meaning of the constants $n_i, \mathbf{V},$ and $T$ is not evident.

You can then show that the distribution function in terms of these constants takes the Maxwell-Boltzmann form $$f_i = n_i \left(\frac{m_i}{2 \pi T} \right)^{3/2} \exp\left[- \frac{m_i(\mathbf{v}_i - \mathbf{V})^2}{2T} \right]$$
Using this form of $f_i$, you find by straightforward integration that
$$\begin{align*}
n_i & = \int f_i \, d^3\mathbf{v}_i \\
n_i \mathbf{V} & = \int \mathbf{v}_i \, f_i \, d^3\mathbf{v}_i\\
\frac 3 2 n_i T & = \int \frac 1 2 m_i \, v_i^2 \, f_i \, d^3\mathbf{v}_i - n_i \frac 1 2 m_i V^2
\end{align*}$$

Note that the last equation here differs from equation (3.55) in the link where the last term is not included. I believe (3.55) in the link is incorrect.

These equations show the physical meaning of the constants $n_i, \mathbf{V},$ and $T$.

Of course, the student could be left scratching her head wondering how anyone would know ahead of time to define the constant $n_i$ by the strange-looking equation $a_i = \ln\left[n_i \left(\frac{m_i}{2 \pi T}\right)^{3/2}\right] - \frac{m_i V^2}{2T}$.
---------------------------------------

Another way to develop this is to define the constants $n_i, \mathbf{V},$ and $T$ by the physically meaningful equations
$$\begin{align*}
n_i & = \int f_i \, d^3\mathbf{v}_i \\
n_i \mathbf{V} & = \int \mathbf{v}_i \, f_i \, d^3\mathbf{v}_i\\
\frac 3 2 n_i T & = \int \frac 1 2 m_i \, v^2 \, f_i \, d^3\mathbf{v}_i - n_i \frac 1 2 m_i V^2
\end{align*}$$ where $f_i$ is the distribution function defined in terms of the constants $a_i, \mathbf{b},$ and $c$ : $$\ln f_i = a_i + m_i \mathbf{b}\cdot \mathbf{v}_i + m_i c v_i^2$$ That is, $$f_i = \exp[ a_i + m_i \mathbf{b}\cdot \mathbf{v}_i + m_i c v_i^2]. $$ Then you can derive the equations
$$\begin{align*}
a_i & = \ln\left[n_i \left(\frac{m_i}{2 \pi T}\right)^{3/2}\right] - \frac{m_i V^2}{2T} \\
b & = \frac{1}{T}\mathbf{V}\\
c & = -\frac{1}{2T}
\end{align*}$$ by carrying out the integrations in
$$\begin{align*}
n_i & = \int f_i \, d^3\mathbf{v}_i \\
n_i \mathbf{V} & = \int \mathbf{v}_i \, f_i \, d^3\mathbf{v}_i\\
\frac 3 2 n_i T & = \int \frac 1 2 m_i \, v^2 \, f_i \, d^3\mathbf{v}_i - n_i \frac 1 2 m_i V^2
\end{align*}$$
For example, with $f_i = \exp[ a_i + m_i \mathbf{b}\cdot \mathbf{v}_i + m_i c v_i^2]$, you can show that $$\begin{align*}
\int f_i \, d^3 \mathbf{v}_i & = \left(\frac{\pi}{m_i|c|} \right)^{3/2} \exp\left[ a_i + \frac{m_ib^2}{4|c|} \right] \\
\int \mathbf{v}_i \, f_i \, d^3 \mathbf{v}_i & = n_i \frac{\mathbf{b}}{2|c|} \\
\int v_i^2 \, f_i \, d^3 \mathbf{v}_i & = n_i \left( \frac{3}{2 m_i |c|} + \frac{b^2}{4c^2} \right)
\end{align*}$$ Using these in the defining relations
$$\begin{align*}
n_i & = \int f_i \, d^3\mathbf{v}_i \\
n_i \mathbf{V} & = \int \mathbf{v}_i \, f_i \, d^3\mathbf{v}_i\\
\frac 3 2 n_i T & = \int \frac 1 2 m_i \, v^2 \, f_i \, d^3\mathbf{v}_i - n_i \frac 1 2 m_i V^2
\end{align*}$$ gives three equations that can be used to derive
$$\begin{align*}
a_i & = \ln\left[n_i \left(\frac{m_i}{2 \pi T}\right)^{3/2}\right] - \frac{m_i V^2}{2T} \\
b & = \frac{1}{T}\mathbf{V}\\
c & = -\frac{1}{2T}
\end{align*}$$
This approach is fairly tedious. But it has the advantage of not having to pull the equation $a_i = \ln\left[n_i \left(\frac{m_i}{2 \pi T}\right)^{3/2}\right] - \frac{m_i V^2}{2T}$ out of thin air.