- #1
member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For part(a),
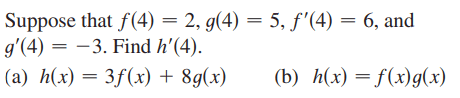
The solution is,
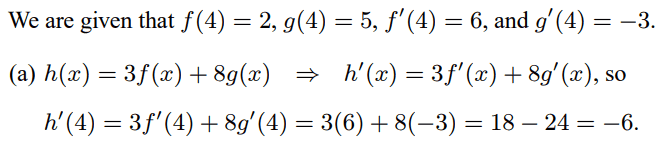
However, why do they not take the derivative of the inner function (if it exists) of f(x) or g(x) using the chain rule? For example if ##f(x) = \sin(x^2)##
Many thanks!
The solution is,
However, why do they not take the derivative of the inner function (if it exists) of f(x) or g(x) using the chain rule? For example if ##f(x) = \sin(x^2)##
Many thanks!