Halting problem is undecidable proof confusion-:

[shivajikobardan]

https://slideplayer.com/slide/10708471/
This is the context I am talking about.

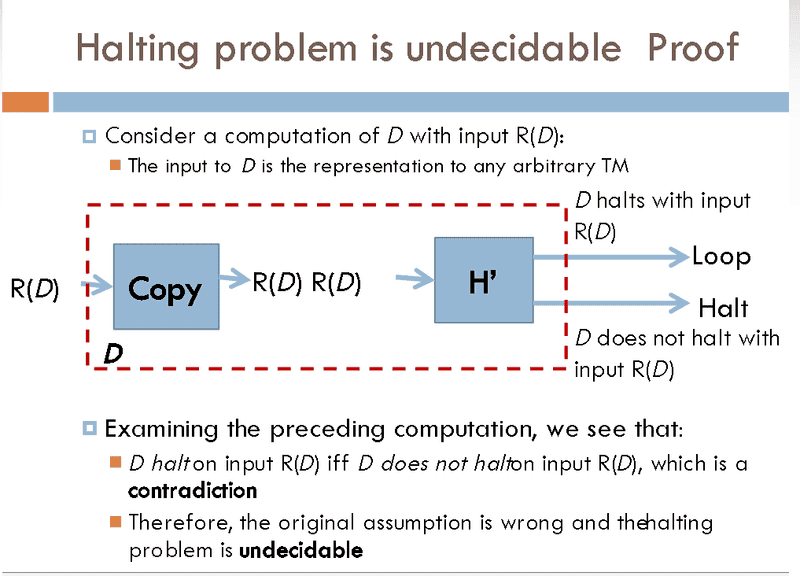
What contradiction occur here? We begin by telling that there is a Turing machine H that solves the halting problem. So how does this contradicts? Can you tell me about that?

What contradiction occur here? We begin by telling that there is a Turing machine H that solves the halting problem. So how does this contradicts? Can you tell me about that?

 

[Evgeny.Makarov]

I write $M(w)$ for the computation of a TM $M$ on inout $w$. The contradiction is as follows. If $D$ halts on $R(D)$, then by the definition of $H'$ we have $H'(R(D), R(D))$ loops. But the latter computation is a part of the computation $D(R(D))$; therefore, $D$ loops on $R(D)$. This is by itself is not a contradiction yet; it just means that $D$ cannot halt on $R(D)$. However, the inversion of that implication also holds: if $D$ loops on $R(D)$, then by the definition of $H'$ we have $H'(R(D), R(D))$ halts. Since this computation is the last portion of $D(R(D))$, the latter computation halts as well. So if we denote "$D$ halts on $R(D)$" by $P$, we get both $P\to\neg P$ (which implies $\neg P$) and $\neg P\to P$, which together with the former implication means $P\leftrightarrow \neg P$. This is a contradiction.