- #1
undividable
- 24
- 0
Is the following logic correct?:
If you have an hamiltonian, that has time has a variable explicitly, and you get the lagrangian,L, from it, and then you get an equivalent L', since L has the total time derivate of a function, both lagrangians will lead to the same equations euler-lagrange equations right? If so, and if you get you get the hamiltonian from L', and you find the hamilton equations from it will they be equal to the original hamiltonian's hamilton equations? and if they are won't the first hamiltonian's hamiltion equation have time explicitly(since the given hamiltonian has time), whereas the second hamiltonian's hamilton equations won't have time(because L' does not have time). how can they be the same?
if it is of any help, the given hamiltonian is :
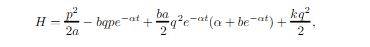
If you have an hamiltonian, that has time has a variable explicitly, and you get the lagrangian,L, from it, and then you get an equivalent L', since L has the total time derivate of a function, both lagrangians will lead to the same equations euler-lagrange equations right? If so, and if you get you get the hamiltonian from L', and you find the hamilton equations from it will they be equal to the original hamiltonian's hamilton equations? and if they are won't the first hamiltonian's hamiltion equation have time explicitly(since the given hamiltonian has time), whereas the second hamiltonian's hamilton equations won't have time(because L' does not have time). how can they be the same?
if it is of any help, the given hamiltonian is :
Attachments
Last edited: