You must be more careful with operator ordering! You should get the last equation on your scanned calculations (BTW, it's much less work and better for the forum to use the built-in LaTeX feature. Click the LaTeX guide (link at the left directly under the text editor):
https://www.physicsforums.com/help/latexhelp/
Concerning the calculation, note that
$$(\hat{a}-\hat{a}^{\dagger})^2=\hat{a}^2 - \hat{a} \hat{a}^{\dagger} - \hat{a}^{\dagger} \hat{a}+ \hat{a}^{\dagger 2}$$
and
$$(\hat{a}+\hat{a}^{\dagger})^2=\hat{a}^2 + \hat{a} \hat{a}^{\dagger} + \hat{a}^{\dagger} \hat{a} + \hat{a}^{\dagger 2}.$$
From that you get
$$(\hat{a}+\hat{a}^{\dagger})^2-(\hat{a}-\hat{a}^{\dagger})^2=2 (\hat{a}\hat{a}^{\dagger} + \hat{a}^{\dagger} \hat{a})=2([\hat{a},\hat{a}^{\dagger}]+2 \hat{a}^{\dagger} \hat{a}]=4 \left (\hat{a}^{\dagger} \hat{a} + \frac{1}{2} \right).$$
Plugging this into your equation for the Hamiltonian, you get your final equation (1),
$$\hat{H}=\hbar \omega \left (\hat{a}^{\dagger} \hat{a} + \frac{1}{2} \right).$$
The additive piece ##\hbar \omega/2 \hat{1}## is just a constant operator commuting with everything, and just counting the energy of the ground state as zero, you get the equivalent Lagrangian
$$\hat{H}'=\hbar \omega \hat{a}^{\dagger} \hat{a},$$
which describes the same physics as the original Hamiltonian, except that your zero level for energy is shifted.
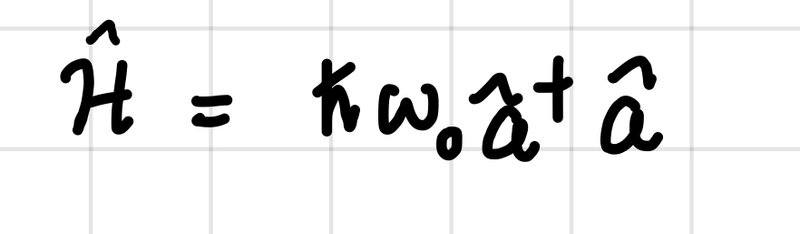 I normally derive the Hamiltonian for a SHO in Hilbert space with a term of 1/2 hbar omega included. However, I am unsure of how one derives this from Hilbert space to Fock space. I have attached my attempt at it as an image below. Any input will be of great help. Cheers.
I normally derive the Hamiltonian for a SHO in Hilbert space with a term of 1/2 hbar omega included. However, I am unsure of how one derives this from Hilbert space to Fock space. I have attached my attempt at it as an image below. Any input will be of great help. Cheers.

