- #1
ballzac
- 104
- 0
I'm preparing for an exam at the moment and in one of the past exams the is a question asking to prove that the hamiltonian operator can be expressed in terms of the ladder operators.
The solution is this
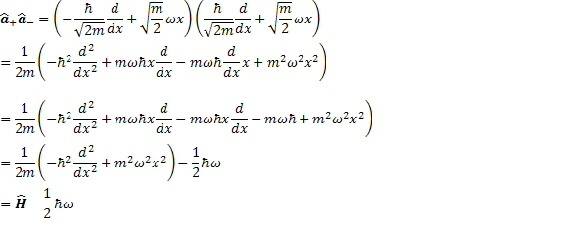
(The minus sign didn't come out in the last line, and obviously there is one more step that I left of the end, but you get the picture.)
Following this from the second to the third line seems to imply

But I would expect

because the derivative of x wrt x is 1. My maths isn't terribly good, and there is obviously something simple that I am missing, but I've been staring at this for days and can't seem to get it. Could someone please explain what I'm missing?
I could answer this question if it comes up on the exam, because I can remember how it goes, but I want to actually be able to understand it.
Thanks in advance.
The solution is this
(The minus sign didn't come out in the last line, and obviously there is one more step that I left of the end, but you get the picture.)
Following this from the second to the third line seems to imply
But I would expect
because the derivative of x wrt x is 1. My maths isn't terribly good, and there is obviously something simple that I am missing, but I've been staring at this for days and can't seem to get it. Could someone please explain what I'm missing?
I could answer this question if it comes up on the exam, because I can remember how it goes, but I want to actually be able to understand it.
Thanks in advance.