Hamiltonian V and T of a lattice?

[James1238765]

TL;DR Summary

How to define potential energy T and kinetic energy V of a lattice grid?

A toy model of a QFT lattice (in 1 dimension) is given in [here] (at 5:55):

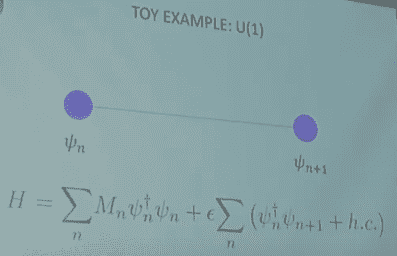
We assume that $\Psi$ is a vector set of four complex numbers having some values at every point on the grid, for instance:

$$\Psi_{100} =
\begin{bmatrix}
1+2i \\
3+4i \\
5+6i \\
7+8i
\end{bmatrix}$$

and

$$\Psi_{101} =
\begin{bmatrix}
11+12i \\
13+14i \\
15+16i \\
17+18i
\end{bmatrix}$$

Then,

$$\Psi_{100}^\dagger \Psi_{100} =
\begin{bmatrix}
1-2i & 3-4i & 5-6i & 7-8i
\end{bmatrix}
\begin{bmatrix}
1+2i \\
3+4i \\
5+6i \\
7+8i
\end{bmatrix}$$
$$= (1^2+2^2) + (3^2+4^2) + (5^2+6^2) + (7^2+8^2) $$

$$= 204 $$

Therefore, the sum of each of this $\Psi_n^\dagger \Psi_n$ scalar real number over all the grid points can be thought of as the total "potential energy" stored in this grid:

$$V := \sum_{grid} \Psi_n^\dagger \psi_n$$

But then,

$$\Psi_{100}^\dagger \Psi_{101} $$

$$=\begin{bmatrix}
1-2i & 3-4i & 5-6i & 7-8i
\end{bmatrix}
\begin{bmatrix}
11+12i \\
13+14i \\
15+16i \\
17+18i
\end{bmatrix}$$
$$= (1-2i)(11+12i) + (3-4i)(13+14i) + (5-6i)(15+16i) + (7-8i)(17+18i) $$
$$= 564 - 40i $$

is a messy complex number.

In what sense can the sum of this quantity $\Psi_n^\dagger \Psi_{n+1}$:

$$T := \sum_{grid} \Psi_n^\dagger \psi_{n+1} $$

be thought of as the "kinetic energy" contained in this grid?

 

[PeterDonis]

In what sense can the sum of this quantity $\Psi_n^\dagger \Psi_{n+1}$:

$$T :=? \sum \Psi_n^\dagger \psi_{n+1} $$

be thought of as the "kinetic energy" contained in this grid?

Does the video you referenced answer this question? Does it give any references you can look at to find the answer?

 

[James1238765]

@PeterDonis The motivation for this definition of H is not explained by the presenter.

 

[PeterDonis]

@PeterDonis The motivation for this definition of H is not explained by the presenter.

That probably means the presenter is expecting the audience to already have that background knowledge. If you don't, that might mean this subject is one you should hold off on digging into until you do.

(Note that you marked this thread as "A" level, which indicates graduate level understanding of the subject matter.)

 

[James1238765]

@PeterDonis H is usually defined as T + V, so there must be some reason $\sum_{grid} \Psi_n^\dagger \Psi_{n+1}$ is chosen to represent T. Even in toy models, people who have thought for years about a problem will often choose some "wisdom" quantities that has depth, based on their experience with the real thing.

 

[Frabjous]

Here are the slides. He references several of his papers.
https://obj.umiacs.umd.edu/cchep17/reznik_slides.pdf

 

[PeterDonis]

@PeterDonis H is usually defined as T + V, so there must be some reason $\sum_{grid} \Psi_n^\dagger \Psi_{n+1}$ is chosen to represent T. Even in toy models, people who have thought for years about a problem will often choose some "wisdom" quantities that has depth, based on their experience with the real thing.

All of this may be true. That doesn't change the fact that the logical place to look for the answer to these questions is in the presentations or papers of the person who built the model.

 

[PeterDonis]

$\sum_{grid} \Psi_n^\dagger \Psi_{n+1}$ is chosen to represent T.

From what I can gather, that is the potential energy, not the kinetic energy. The kinetic energy is the $\Psi_n^\dagger \Psi_n$ term.

 

[James1238765]

@PeterDonis thank you. I guess the H can be thought of as the combination of a self-energy term, and adjacent-energy-difference term. A wavefunction $\Psi$ will time evolve based only on the current density of the excitations at each point, and also how the adjacent-density-difference looks like between neighboring points (Dirac equation).

Suppose a completely empty field (0 numbers everywhere), with just 1 particle created (ie. 8 excitation numbers) at one location x. No matter how x is moved within the grid, the term H is constant in this empty field. So, something is conserved, aka energy.

 

[PeterDonis]

I guess the H can be thought of as the combination of a self-energy term, and adjacent-energy-difference term.

Yes, with the self-energy term being the kinetic energy and the adjacent energy difference term being the potential energy. The fact that the self-energy term has a coefficient $M_n$ supports this interpretation, since I assume that's the mass of the object at lattice point $n$.

 

[DrClaude]

We assume that Ψ is a vector set of four complex numbers having some values at every point on the grid, for instance:

That's incorrect. This is a second quantization formulation. The $\psi$ are operators.

 

[James1238765]

@DrClaude thank you. How many numbers should represent the field excitations at each grid point, in the second quantization formulation?

 

[PeterDonis]

@DrClaude thank you. How many numbers should represent the field excitations at each grid point, in the second quantization formulation?

This is the sort of question someone who posts an "A" level thread should already know the answer to. Most introductory textbooks on quantum field theory discuss this.

 

[malawi_glenn]

Most introductory textbooks on quantum field theory discuss this.

For instance... ?

@James1238765 check out https://saalburg.aei.mpg.de/wp-content/uploads/sites/25/2017/03/wiese.pdf

 

[James1238765]

@malawi_glenn thank you for the reference. A scalar valued field is given as a first field in on page 29. The action $S$ on this field $\Phi$ is constructed with the form:

$$ S = \sum_{grid} \Phi_x M \Phi_y $$

I gather M is a coupling matrix, with line by line entries specifying the preset coupling factors between any two points on the grid.

From this 1-line definition (page 29), I am not quite clear how exactly is this model suppose to time evolve? What is propelling the grid to change from t to t+1? M has fixed values. The scalar values $\Phi$ is preset for each individual point. What is going to drive the time evolution of this model?

@PeterDonis The main trouble I have with physics texts is that most texts are not written to instruct how to construct the model in question; they are written instead to show how to *use* the model. Often there is a mismatch between the kinds of low level implementation details needed to construct the model, versus the kinds of high level theorems given to use the model.

 

[hutchphd]

The main trouble I have with physics texts is that most texts are not written to instruct how to construct the model in question; they are written instead to show how to *use* the model.

That is why you need to learn to walk before you learn to fly. Your flight instructor will assume certain things.
Books would be very thick if absolutely self-contained.

 

[James1238765]

A post to expand on the implementer's point of view (there aren't many espousing this): So in our machine we have space for 100,000,000,000 entries of any types of numbers. We also have an arithmetic logic unit whose capabilities are only two: 1. add two numbers 2. compare two numbers.

All those symbolic algebra, integration, and theorems eventually is not usable directly, and has to be translated into these very basic structures. As implementers, we often would rather a direct prescription what numbers to put initially into the data fields, and what basic arithmetic sequence of computation to make.

We can often judge whether our system works and what behavior it will possess. So i guess the implementer's dream is essentially, give us a clear prescription, let us build the model first, and we can go and analyze it together.

 

[PeterDonis]

The main trouble I have with physics texts is that most texts are not written to instruct how to construct the model in question; they are written instead to show how to *use* the model.

I'm not sure what you mean. Physics texts tell you how to make calculations using the model; that means telling you the equations and what the symbols in the equations mean. What else is there to "constructing" the model?

The trouble you are having is that you are not using physics texts, you're using videos, and you're starting with very advanced topics without having the background necessary to understand them. It's as if you tried to look at calculus when you haven't even learned basic arithmetic. A description of how to "construct a model" using calculus that would be perfectly understandable to someone with the necessary background, is not going to be understandable to someone who hasn't even learned basic arithmetic. That's why physics pedagogy teaches the basics first, before teaching the advanced topics that you need the basics to understand.

 

[PeterDonis]

A scalar valued field is given as a first field in on page 29.

Before you got to page 29, did you read the preceding pages? Did you understand them?

 

[James1238765]

@PeterDonis Returning to the question at hand, from

$$ S = m_{xy} \Phi_x \Phi_y $$

on page 29, I am not quite clear how exactly is this model supposed to time evolve? What is propelling the grid to change from t to t+1? $M_{xy}$ has fixed values. The scalar values $\Phi_x$ is preset for each individual point. What is going to drive the time evolution of this model?

 

[PeterDonis]

I am not quite clear how exactly is this model supposed to time evolve?

That's why I asked you if you had read the pages before page 29. There is a lot of pertinent information there that is relevant to your question.

 

[James1238765]

@PeterDonis the model is a toy model. I do not see how 100 years of QFT is needed to explain a toy model.

The question is simple. If you indeed know the answer, a quick answer in 1 or 2 sentences will do. I have some inklings by the way: the H being constant over time will be used as a constraint to force the time evolution in some manner. I pose the question naively to force a clear minded answer from someone who is in a more expert position to clarify what this time-evolution procedure might look like for this toy model.

 

[PeterDonis]

the model is a toy model. I do not see how 100 years of QFT is needed to explain a toy model.

I didn't say 100 years of QFT. I only asked if you had read pages 1 through 28, i.e., the pages before 29, in the reference that @malawi_glenn gave you.

The question is simple.

So is the one I asked you. Since you are persistently refusing to answer it, I am going to guess that the answer is no. How do you expect to understand page 29 if you haven't read pages 1 through 28? And if you're unwilling even to do that, i.e., to actually read a reasonably brief reference you were given specifically in response to a question of yours, why should we keep this thread open?

a quick answer in 1 or 2 sentences will do

Only until you ask your next question. How many questions will it take until you actually understand this topic? And how much time will that involve compared to taking a course in QFT? PF's purpose is not to give comprehensive teaching on a subject. We expect you to do the bulk of the work of learning yourself.

 

[PeterDonis]

I have some inklings by the way

Before having any inklings at all, you might ask yourself this question (the answer to which you would know if you have read pages 1 through 28 of the reference you were given): what do the lattice points represent? What are they points of?

 

[James1238765]

@PeterDonis there are no scalar fields, other than the Higgs field, is there? Do you mean this toy model describes the Higgs?

The numbers don't mean anything to me. It is a toy model. It is just a set of numbers, which can be time evolved according to made up rules. My question is, give an explicit example of this made-up time evolution rule?

 

[PeterDonis]

there are no scalar fields, other than the Higgs field, is there?

If you mean in our current Standard Model of particle physics, the Higgs field is the only fundamental scalar field. However, there are many composites, such as a number of mesons, which are scalar.

Do you mean this toy model describes the Higgs?

I have said no such thing. If you read the reference you were given, it will tell you the intended purpose of the toy model you are asking about.

The numbers don't mean anything to me.

Yes, because you aren't actually reading the reference, you're just grabbing equations out of it and asking questions about them with no context and no background knowledge.

 

[James1238765]

@PeterDonis I am a simple man, I guess. To me either the answer satisfies the question, or it does not.

 

[PeterDonis]

To me either the answer satisfies the question, or it does not.

Can you give a satisfactory answer to the question I asked in post #24?

 

[James1238765]

@PeterDonis I will try:

Page 1 -12 (Introduction and Motivation) is preamble targeted at getting the reader to give the text a chance and continue reading. I am already reading, because I want a concrete lattice model, so this is saved for later.

Page 13-15 starts with Newton's F=ma, and show how to derive the same using Euler Lagrange functional variation inflection points. It went to say how to discretize the Lagrangian. (Yes, I have implemented and time-evolved the Schrodinger equation; we replace the differentials with finite difference quantites is all).

Page 16-21 describes the path integral approach. I know this to be an equivalent formulation (and that there are many equivalent formulations in QM). I am not familiar with the details of path integral approach, if it's equivalent then I shall just stick to the Schrodinger style wave/field function approach.

Page 22 "describes" the Ising spin model (which I have implemented before). It does this with symbolic algebra manipulation, which does not clarify or help me solve an earlier question about how to represent spin concretely on a toric code lattice.

Page 23-27 goes on into the mathematical properties of the discrete H "transfer matrix". When implementing things, I do not immediately need the mathematical proofs that it is commutative, associative, or distributive. I saved this for future proof reading.

Page 28-29 arrives at the first simplest model of a lattice discrete grid. Now my line of thinking is to divorce everything used to arrive at this model. Let's start the blank state with this model and only this, nothing else, and start to investigate its properties.

Thus, here we are now at page 29.

 

[PeterDonis]

my line of thinking is to divorce everything used to arrive at this model

That's not a good idea since answers to questions you are asking are in the information you are now "divorcing".

 

[James1238765]

@PeterDonis Can you give a similarly straight answer for the question i posed in #20?

"Do. Or do not. There is no try." -Yoda

 

[PeterDonis]

I am not familiar with the details of path integral approach, if it's equivalent then I shall just stick to the Schrodinger style wave/field function approach.

The Schrodinger style approach does not even exist for quantum field theory. QFT is not the same as non-relativistic QM. That's why many QFT texts start with the path integral approach. The other common approach to QFT is canonical quantization, which is where the term "second quantization" that @DrClaude used comes from. But that's not the Schrodinger approach either.

 

[James1238765]

@PeterDonis yes, I have implemented the Dirac spinor 4-wavefunctions too... I understand that the fields in QFT must be Lorentz invariant to qualify... implementation-wise though all these are very similar to do, so I tend to make no distinctions (the fields are wavefunctions implementationally).

 

[PeterDonis]

Can you give a similarly straight answer for the question i posed in #20?

I could, but I won't, because I think you would be better served by taking the huge hint I have already given you (in the question I asked in post #24) and figuring it out for yourself.

 

[PeterDonis]

the fields are wavefunctions implementationally

No, they aren't. @DrClaude already told you that in post #11.