Has anyone seen this logarithmic spiral creation before?

[dave202]

<Moderator's note: Image added because otherwise the thread might once become unreadable.>

I have reason to believe this could have applications in physics, but right now it's just a mathematical result I came across recently. Either way, I think it is very interesting and fun to look at.

This is my best attempt at explaining it in words:

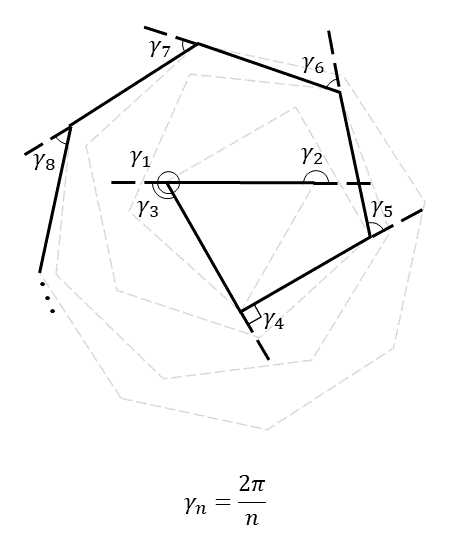
The curve generated by a series of unitary line segments placed end to end with a deviation angle given by the harmonic series, γ_n=2π/n, approximates a logarithmic spiral given by the polar equation r=e^θ/2π. This “angular harmonic” series (γ_n=2π/n) is the series of external angles of all regular polygons, where n is the number of sides.

More generally, the deflection angle can be given by any scalar multiple of the harmonic series, i.e. γ_n=x/n, for any real (or imaginary?) number x. In this general case, the curve approximates a spiral given by the equation r=e^θ/x.

Figures:
https://imgur.com/a/ZBAF2

 

[kuruman]

I have seen this spiral as a solution to the following problem.
Imagine N mice on the vertices of a regular N-gon of side $a$. Each mouse moves straight towards the mouse in front of it at constant speed v. Eventually the mice converge to a point (they are point mice). Find the distance covered by one mouse from start to finish.

If you draw the path of all the mice, you get N spirals of the kind you show. You can also show that in the limit N → ∞, the mice run around in a circle as expected. The secret to solving this problem is to notice that, by symmetry, the shape of the N-gon is preserved which means that the radial velocity of the mice is constant and v_r = v*cosθ_N, where θ_N is the angle between side $a$ and the radius. You can fill in the rest of the details if you are interested.