(has been resolved)：Integral to find elbow volume

[tracker890 Source h]

Homework Statement

to find elbow volume

Relevant Equations

volume integral

has been resolved

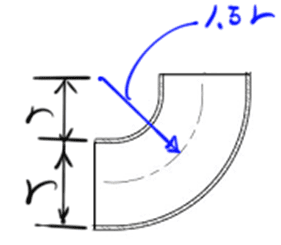
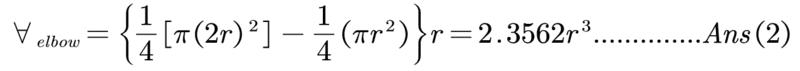
Please help me to understand which answer is correct.
I use the integral method to find the elbow volume as follows：

But my book say：

 

[Lnewqban]

The area of the circular cross-section of diameter r shown in the integral is not correct, it should be $\pi(r)^2/4$

 

[tracker890 Source h]

The area of the circular cross-section of diameter r shown in the integral is not correct, it should be $\pi(r)^2/4$

i think it should be $\pi(2r)^2/4$

 

[Lnewqban]

i think it should be $\pi(2r)^2/4$

Think again…
The r that has been given to you is the diameter of the cross-section of the elbow.
Therefore, the area of that section should be π times the radius of that section, which in your case is r/2.
Then,
$\pi(r/2)^2=\pi(r)^2/4$

 

[Lnewqban]

Another way to do it, leading to the same result of $2.3562*r^3$ that is shown in the book:
Straightening the elbow until it becomes a cylinder, its length should be equal to the perimeter of the center line of the elbow.
As the perimeter of that line is $2\pi(radius~to~center)/4$, then
$Length=2\pi(1.5r)/4$
$Volume=Area~*~Length$
$Volume=(\pi/4)[(r^2)(2)(1.5)(r)]=(3/4)\pi(r^3)$

 

[Frabjous]

Another way to do it, leading to the same result of $2.3562*r^3$ that is shown in the book:
Straightening the elbow until it becomes a cylinder, its length should be equal to the perimeter of the center line of the elbow.
As the perimeter of that line is $2\pi(radius~to~center)/4$, then
$Length=2\pi(1.5r)/4$
$Volume=Area~*~Length$
$Volume=(\pi/4)[(r^2)(2)(1.5)(r)]=(3/4)\pi(r^3)$

Shouldn’t there be another π/4?

 

[Lnewqban]

Shouldn’t there be another π/4?

Perhaps.
I am very clumsy working with LaTeX.

 

[tracker890 Source h]

Perhaps.
I am very clumsy working with LaTeX.

View attachment 319111

Your answer is correct.
The cross section area = $\pi \text{(}\frac{r}{2}\text{)}^2$
$$
\forall _{elbow}=\int_0^{\frac{\pi}{2}}{A\left( 1.5r \right) d\theta =}\int_0^{\frac{\pi}{2}}{\left( \pi \text{(}\frac{r}{2}\text{)}^2 \right) \left( \frac{3}{2}r \right) d\theta =\text{(}\frac{\pi r^2}{4}\text{)}\left( \frac{3}{2}r \right) \left( \frac{\pi}{2} \right)}=\frac{3}{16}\pi ^2r^3
$$

 

[tracker890 Source h]

Think again…
The r that has been given to you is the diameter of the cross-section of the elbow.
Therefore, the area of that section should be π times the radius of that section, which in your case is r/2.
Then,
$\pi(r/2)^2=\pi(r)^2/4$

Yes!
Your answer is correct.