Elmo
- 37
- 6
- TL;DR Summary
- A confusion about the Feynman rule for the HQET propagator.
I have a confusion about how the heavy quark propagators are constructed in HQET and how the loops (in the included figure) are constructed.
A standard sort of introduction and motivation to HQET (as in reviews and texts like Manohar & Wise and M.D Schwartz) is as follows :
The momentum of a heavy quark interacting with soft particles is #p^{\mu}=Mv^{\mu}+k^{\mu}# and the derivation of the heavy quark propagator from its corresponding form in QCD is thus :
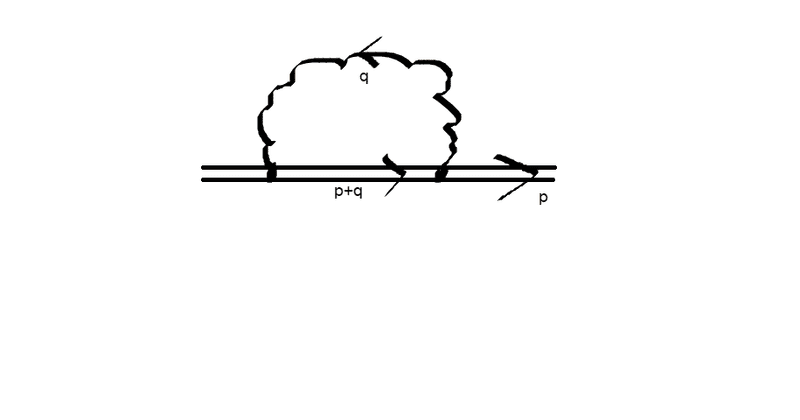
\slashedp+\slashedk+M(p−k)2−M2∼M(1+\slashedv)2Mv.k . The thing which makes it tick is the fact that #k^{\mu}# is soft and #M# is hard. This is all fine but I dont understand how we can apply the same logic to get the following loop correction in the figure (which is also solved in multiple sources).
Σ∼∫dDq1[q2][v.(p+q)]If we write the same quark propagator from QCD and work onwards from that :
\slashedp+\slashedq+M(p+q)2−M2∼M(1+\slashedv)+\slashedqq2+2Mv.q
Here we cant take q to be soft can we, as its spans all regions of the loop momentum.
A standard sort of introduction and motivation to HQET (as in reviews and texts like Manohar & Wise and M.D Schwartz) is as follows :
The momentum of a heavy quark interacting with soft particles is #p^{\mu}=Mv^{\mu}+k^{\mu}# and the derivation of the heavy quark propagator from its corresponding form in QCD is thus :
\slashedp+\slashedk+M(p−k)2−M2∼M(1+\slashedv)2Mv.k . The thing which makes it tick is the fact that #k^{\mu}# is soft and #M# is hard. This is all fine but I dont understand how we can apply the same logic to get the following loop correction in the figure (which is also solved in multiple sources).
Σ∼∫dDq1[q2][v.(p+q)]If we write the same quark propagator from QCD and work onwards from that :
\slashedp+\slashedq+M(p+q)2−M2∼M(1+\slashedv)+\slashedqq2+2Mv.q
Here we cant take q to be soft can we, as its spans all regions of the loop momentum.