Heights and distances problems

[Drain Brain]

I got stuck with these problems from my trig book.
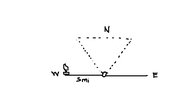
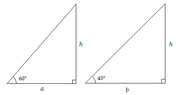
first I would like to elaborate what part of the problem is difficult for me. For the first problem I'm having a hard time producing a picture of the situation. Secondly, is the problem asking about a particular ratio? Maybe what's really hurting me the most is my reading comprehension since English is not my first language. I'm hoping that you can bear with that.

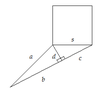
Now, for the second problem I tried drawing a picture of the situation given, but I am not quite sure if it is correct.

Here,
View attachment 3486

I couldn't deduce anything from this. Thanks!

 

[MarkFL]

Here is a diagram to help get you started with the first problem:

View attachment 3487

If we let $h$ be the height of the tower, then what is $a$ in terms of $h$? What is $b+c$?

 

[MarkFL]

A better approach (in my opinion) would be to use the following diagram:

View attachment 3488

Now find $a$ and $b$ in terms of $h$, and $c$ in terms of $s$, then apply the Law of Cosines as follows:

$$s^2=a^2+b^2-2ab\cos(\theta)$$

$$c^2=b^2+b^2-2b^2\cos(2\theta)$$

From this, you can determine the ratio $$\frac{h}{s}$$.

You may need $$\left(\sqrt{5}+1\right)^2=6+2\sqrt{5}$$. :D

 

[soroban]

Hello, Drain Brain!

19. lighthouse facing north sends out a fan-shaped beam of light extending from NE to NW.
A steamer sailing due west first sees the lighthouse when it is 5 miles from the lighthouse
and continues to see it for 30\sqrt{2} minutes. .What is the speed of the steamer?

                   _
                 5√2
         B * - - - - - - - * A
            *            *
             5 *       * 5
                 * 90*
       - - - - - - * - - - - - -

The steamer travels from A to B.
We have an isosceles right triangle;
Its hypotenuse s 5\sqrt{2}.

The steamer travels 5\sqrt{2} miles in 30\sqrt{2} minutes \;=\:\tfrac{\sqrt{2}}{2} hours.

Therefore, its speed is: .\frac{5\sqrt{2}}{\frac{\sqrt{2}}{2}} \:=\:10 miles per hour.

 

[Drain Brain]

I still don't get the method for solving problem 18. But what I did as an attempt is to create three different right triangles that lie on different planes the first two trianlges have one of their angle to be 45 degrees and the last one has 60 degrees . As I observed the heights of these three triangles are all the same and their heights refers to the height of the building.

I write the hypotenuse of first two triangles in terms of its height h. I found it to be $h\sqrt{2}$

Now, the hypotenuse of the last trianlge in terms of h is found to be $\frac{2h}{\sqrt{3}}$

I'm not quite sure how to relate all these infos that I get. Please help.

- - - Updated - - -

Hello, Drain Brain!

                   _
                 5√2
         B * - - - - - - - * A
            *            *
             5 *       * 5
                 * 90*
       - - - - - - * - - - - - -

The steamer travels from A to B.
We have an isosceles right triangle;
Its hypotenuse s 5\sqrt{2}.

The steamer travels 5\sqrt{2} miles in 30\sqrt{2} minutes \;=\:\tfrac{\sqrt{2}}{2} hours.

Therefore, its speed is: .\frac{5\sqrt{2}}{\frac{\sqrt{2}}{2}} \:=\:10 miles per hour.

Hi soroban!

How did you know that there is 90 degrees subtended by line joining A and B?

 

[MarkFL]

To determine $a$ and $b$, use the diagram:

View attachment 3489

And $c$ is the diagonal of a square, having side lengths $s$.

Using this information, what do the two equations from the Law of Cosines become?

 

[Drain Brain]

To determine $a$ and $b$, use the diagram:

View attachment 3489

And $c$ is the diagonal of a square, having side lengths $s$.

Using this information, what do the two equations from the Law of Cosines become?

Hi MarkFl, just want to clarify something here, are you looking at the situation from the top of the building? I'm mean Top-view perspective.

 

[MarkFL]

The first two images I drew are a top-down perspective...this latest image is from the side.

 

[Drain Brain]

The first two images I drew are a top-down perspective...this latest image is from the side.

Okay. Doing what you said in post #3

I express a & b in terms of h and I found that $a=\frac{h}{\sqrt{3}}$ and $b=h$. Now expressing c in terms of s, I got $c=s\sqrt{2}$. $\displaystyle s^2=(\frac{h}{\sqrt{3}})^2+h^2-2(\frac{h}{\sqrt{3}})h\cos(\theta)$

$\displaystyle c^2=h^2+h^2-2h^2\cos(2\theta)$

what to do next?

 

[MarkFL]

Replace $c$ with $\sqrt{2}h$ and simplify your equations some, then apply the double angle identity for cosine:

$$\cos(2\theta)=2\cos^2(\theta)-1$$

What you are looking for is to solve for $$\frac{h}{s}$$.

 

[Drain Brain]

Replace $c$ with $\sqrt{2}h$ and simplify your equations some, then apply the double angle identity for cosine:

$$\cos(2\theta)=2\cos^2(\theta)-1$$

What you are looking for is to solve for $$\frac{h}{s}$$.

how did you get $c=\sqrt{2}h$?

when I replaced c with $\sqrt{2}h$ I get,

$(\sqrt{2}h)^2=h^2+h^2-2h^2\cos2\theta$

$2h^2=2h^2-2h^2\cos2\theta$

factoring out $2h^2$

$2h^2=2h^2(1-\cos2\theta)$

$1=(1-(2\cos^{2}\theta-1)$

$1=2(1-\cos^{2}\theta)= 2\sin^{2}\theta$? the h disappeared? what happened?

 

[MarkFL]

I meant $c=\sqrt{2}s$.

 

[Drain Brain]

I meant $c=\sqrt{2}s$.

replacing $c=\sqrt{2}s$

I get after simplifying $s^2=2h^2\sin^{2}\theta$

$2h^2\sin^{2}\theta= (\frac{h}{\sqrt{3}})^2+h^2-2(\frac{h}{\sqrt{3}})h\cos(\theta)$

$2h^2\sin^{2}\theta=\frac{h^2(4\sqrt{3}-6\cos\theta)}{3\sqrt{3}}$ but from this $h^2$ will disappear. how is that?

 

[MarkFL]

I get:

$$s^2=h^2\left(\frac{4-2\sqrt{3}\cos(\theta)}{3}\right)\tag{1}$$

$$s^2=h^2\left(1-\cos(2\theta)\right)\tag{2}$$

Now, apply the double-angle identity for cosine I gave above to (2), then solve (2) for $\cos(\theta)$, and substitute into (1), and then solve for $$\frac{h}{s}$$. :D

 

[Drain Brain]

that's what I did above.

 

[MarkFL]

that's what I did above.

No, you somehow introduced $\sin(\theta)$...

 

[Drain Brain]

No, you somehow introduced $\sin(\theta)$...

okay, I know this is getting very long . :)

$2h^2(1-\cos^2\theta)= h^2\left(\frac{4-2\sqrt{3}\cos(\theta)}{3}\right)\tag{1}$

$2-2\cos^{2}\theta=\left(\frac{4-2\sqrt{3}\cos(\theta)}{3}\right)$

$6-6\cos^{2}\theta=4-2\sqrt{3}\cos\theta$

$6-4=6\cos^{2}\theta-2\sqrt{3}\cos\theta$

$2=6\cos^{2}\theta-2\sqrt{3}\cos\theta$

$6\cos^{2}\theta-2\sqrt{3}\cos\theta-2$

solving for $\cos\theta$ using quadratic formula

I get $\cos\theta=\frac{\sqrt{3}+\sqrt{15}}{6}$

is this correct?

 

[MarkFL]

You don't need to find the numeric value of $\cos(\theta)$...use (2) to get it in terms of $h$ and $s$, then substitute into (1), and then solve for $$\frac{h}{s}$$.

 

[MarkFL]

Here is one way to finish up...

Spoiler

So, (2) becomes (applying the double-angle identity for cosine)

$$s^2=h^2\left(1-(2\cos^2(\theta)-1)\right)$$

$$s^2=h^2\left(2-2\cos^2(\theta)\right)$$

$$\left(\frac{h}{s}\right)^2=\frac{1}{2-2\cos^2(\theta)}$$

From (1), we find:

$$\cos(\theta)=\frac{4-3\left(\dfrac{h}{s}\right)^{-2}}{2\sqrt{3}}$$

Hence:

$$\left(\frac{h}{s}\right)^2=\frac{1}{2-2\left(\dfrac{4-3\left(\dfrac{h}{s}\right)^{-2}}{2\sqrt{3}}\right)^2}$$

$$\left(\frac{h}{s}\right)^2=\frac{1}{2-\dfrac{16-24\left(\dfrac{h}{s}\right)^{-2}+9\left(\dfrac{h}{s}\right)^{-4}}{6}}$$

$$\left(\frac{h}{s}\right)^2=\frac{6}{-4+24\left(\dfrac{h}{s}\right)^{-2}-9\left(\dfrac{h}{s}\right)^{-4}}$$

$$-4\left(\frac{h}{s}\right)^2+18-9\left(\dfrac{h}{s}\right)^{-2}=0$$

$$4\left(\frac{h}{s}\right)^4-18\left(\frac{h}{s}\right)^2+9=0$$

Applying the quadratic formula (and discarding the smaller root since we must have $h>s$), we find:

$$\left(\frac{h}{s}\right)^2=\frac{9+3\sqrt{5}}{4}$$

Thus:

$$\frac{h}{s}=\frac{\sqrt{9+3\sqrt{5}}}{2}=\frac{\sqrt{6}\sqrt{6+2\sqrt{5}}}{4}=\frac{\sqrt{6}\sqrt{\left(\sqrt{5}+1\right)^2}}{4}=\frac{\sqrt{6}\left(\sqrt{5}+1\right)}{4}$$

 

[soroban]

Hello, Drain Brain! Updated - - -

Hi soroban!

How did you know that there is 90 degrees subtended by line joining A and B?

      B * - - - - - - - * A 
          *           * 
            *       *
           45 *   * 45 
      W - - - - * - - - - E
                L

We are told that LA is in the northeasterly direction.
. . Hence: \angle ALE = 45^o

We are told that LB is in the northwesterly direction.
. . Hence: \angle BLW = 45^o

Got it?